EASY

Earn 100

Initial phase of the particle executing SHM with $y = 4 \sin ω t + 3 \cos ω t$ is:

50% studentsanswered this correctly

Important Questions on Simple Harmonic Motion

HARD

Physics>Oscillations and Waves>Simple Harmonic Motion>Equation of SHM

A particle performs linear SHM. At a particular instant, the velocity of the particle is

u

and acceleration is

α

(both having the same direction). At another instant velocity is

v

and acceleration is

β (0 < α < β)

(both in opposite direction to each other).The distance between the two positions is

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Equation of SHM

A particle is executing a simple harmonic motion. Its maximum acceleration is

α

and maximum velocity is

β

. Then, its time period of vibration will be:

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Equation of SHM

A particle is executing SHM along a straight line. Its velocities at distances

x_{1}

and

x_{2}

from the mean position are

V_{1}

and

V_{2}

respectively. Its time period is:

MEDIUM

Physics>Oscillations and Waves>Simple Harmonic Motion>Equation of SHM

A particle performs simple harmonic motion with amplitude A. Its speed is tripled at the instant that it is at a distance

\frac{2 A}{3}

from equilibrium position. The new amplitude of the motion is:

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Equation of SHM

A particle is performing SHM starting from extreme position. Graphical representation shows that, between displacement and acceleration, there is a phase difference of

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Equation of SHM

A particle executes linear simple harmonic motion with an amplitude of 3 cm. When the particle is at 2 cm from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then its time period in seconds is

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Equation of SHM

Which of the following plots represents schematically the dependence of the time period of a pendulum if measured and plotted as a function of its oscillations? (Note: amplitude need not be small)

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Equation of SHM

The oscillation of a body on a smooth horizontal surface is represented by the equation,

X = A \cos (ω t)

, where

X =

displacement at time

t

ω =

frequency of oscillation,

a =

acceleration at time

t

and

T =

time period.
Which one of the following graph shows correctly the variation

a

with

t

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Equation of SHM

The weight suspended from a spring oscillates up and down. The acceleration of weight will be zero at

HARD

Physics>Oscillations and Waves>Simple Harmonic Motion>Equation of SHM

A particle executes simple harmonic motion with an amplitude of

5 cm

. When the particle is at

4 cm

from the mean position, the magnitude of its velocity in

SI

units is equal to that of its acceleration. Then, its periodic time in seconds is:

MEDIUM

Physics>Oscillations and Waves>Simple Harmonic Motion>Equation of SHM

Two particles are performing simple harmonic motion in a straight line about the same equilibrium point. The amplitude and time period for both particles are same and equal to

A

and

T

, respectively. At time

t = 0

one particle has displacement

A

while the other one has displacement

- \frac{A}{2}

and they are moving towards each other. If they cross each other at time

t

, then

t

is:

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Equation of SHM

A simple pendulum of length

L

has mass

M

and it oscillates freely with amplitude

A

. At the extreme position, its potential energy is (

g

= acceleration due to gravity)

MEDIUM

Physics>Oscillations and Waves>Simple Harmonic Motion>Equation of SHM

In an engine the piston undergoes vertical simple harmonic motion with amplitude 7cm. A washer rests on top of the piston and moves with it. The motor speed is slowly increased. The frequency of the piston at which the washer no longer stays in contact with the piston, is close to :

HARD

Physics>Oscillations and Waves>Simple Harmonic Motion>Equation of SHM

The ratio of maximum acceleration to maximum velocity in a simple harmonic motion is

10 s^{- 1} .

At,

t = 0

the displacement is

5 m .

What is the maximum acceleration? The initial phase is

\frac{π}{4}

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Equation of SHM

The radius of circle, the period of revolution, initial position and sense of revolution are indicated in the figure.
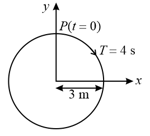
Question Image

y

-projection of the radius vector of rotating particle

P

HARD

Physics>Oscillations and Waves>Simple Harmonic Motion>Equation of SHM

A piston is performing

S . H . M .

in the vertical direction with a frequency of

0.5 Hz

. A block of

10 kg

is placed on the piston. The maximum amplitude of the system such that the block remains in contact with the piston is

HARD

Physics>Oscillations and Waves>Simple Harmonic Motion>Equation of SHM

A particle is performing a linear simple harmonic motion of amplitude

A

. When it is midway between its mean and extreme position, the magnitudes of its velocity and acceleration are equal. What is the periodic time of the motion?

MEDIUM

Physics>Oscillations and Waves>Simple Harmonic Motion>Equation of SHM

The position co-ordinates of a particle moving in a $3 D$ coordinate system is given by

$x = a \cos ω t$

$y = a \sin ω t$

and $z = a ω t$

The speed of the particle is:

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Equation of SHM

The bob of a simple pendulum has mass

2 g

and a charge of

5.0 μ C .

It is at rest in a uniform horizontal electric field of intensity

2000 V / m

At equilibrium, the angle that the pendulum makes with the vertical is:

(t a k e g = 10 m / s^{2})

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Equation of SHM

A particle of mass

m

is moving along the

x - a x i s

under the potential

V (x) = \frac{k x^{2}}{2} + \frac{λ}{x^{'}}

where

k

and

x^{'}

are positive constants of appropriate dimensions. The particle is slightly displaced from its equilibrium position. The particle oscillates with the angular frequency

(ω)

given by

Initial phase of the particle executing SHM with y=4sinωt+3cosωt is:

Important Questions on Simple Harmonic Motion

Learn and Prepare for any exam you want !

Initial phase of the particle executing SHM with $y = 4 \sin ω t + 3 \cos ω t$ is: