Knowledge of phase difference is vital in understanding how waves combine in space-remind yourself by writing down the phase difference of two particles oscillating in step, and two particles oscillating in antiphase.

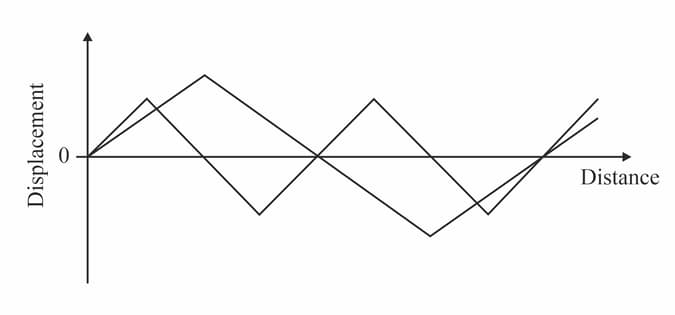
On graph paper, draw two 'triangular' waves similar to those shown in Figure. (These are easier to work with than sinusoidal waves.) One should have wavelength $8.0 \mathrm{cm}$ and amplitude $2.0 \mathrm{cm}$. The other should have wavelength $16.0 \mathrm{cm}$ and amplitude $3.0 \mathrm{cm}$

Use the principle of superposition of waves to determine the resultant displacement at suitable points along the waves, and draw the complete resultant wave.

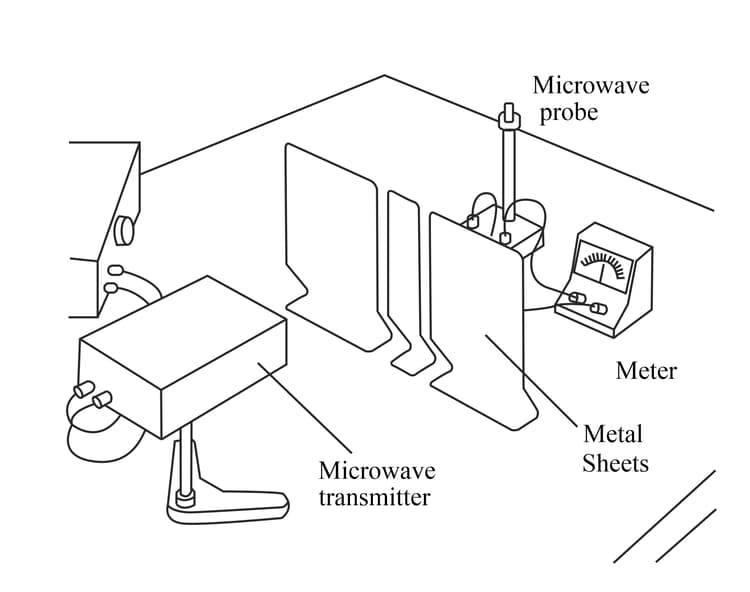
A microwave oven (Figure) uses microwaves with a wavelength of $12.5 \mathrm{cm}$. The front door of the oven is made of glass with a metal grid inside; the gaps in the grid are a few millimetres across. Explain how this design allows us to see the food inside the oven, while the microwaves are not allowed to escape into the kitchen (where they might harm us).

A microwave oven has a metal grid in the door to keep microwaves in and let light out

Look at the experimental arrangement shown in Figure. Suppose that the microwave pro be is placed at a point of low intensity in the interference pattern.

Suggest what will happen if one of the gaps in the barrier is now blocked.

Draw sketches of displacement against time to illustrate the following:

(a) Two waves having the same amplitude and in phase with one another

Draw sketches of displacement against time to illustrate the following:

(b) Two waves having the same amplitude and with a phase difference of $90°$.

Draw sketches of displacement against time to illustrate the following:

(c) Two waves initially in phase but with slightly different wavelengths.

Consider points $\mathrm{D}$ and $\mathrm{E}$ on the screen in Figure, where $\mathrm{BC}=\mathrm{CD}=\mathrm{DE}$. State and explain what you would expect to observe at $\mathrm{D}$ and $\mathrm{E}$.

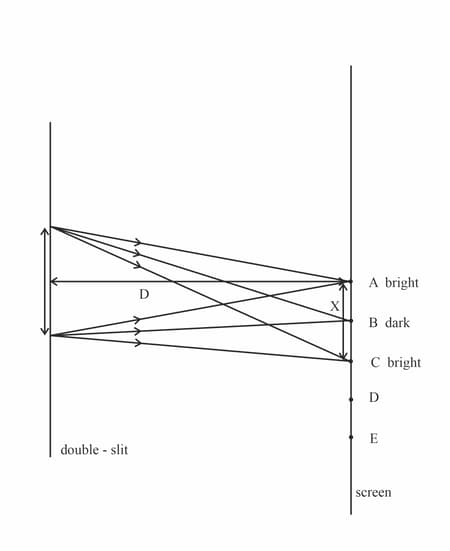
The type of interference, and hence whether a bright or a dark fringe is seen on the screen, depends on the path difference between the rays of light arriving at the screen from the double-slit.