The locus of the point of intersection of the lines 2 x - y + 4 2 k = 0 and 2 k x + k y - 4 2 = 0 ( k is any non-zero real parameter) is

a hyperbola with length of its transverse axis 8 2

an ellipse whose eccentricity is 1 3

a hyperbola whose eccentricity is 3

an ellipse with length of its major axis 8 2

HARD

Earn 100

Let $B C$ be a fixed line segment in the plane. The locus of a point $A$ such that the triangle $A B C$ is isosceles, is (with finitely many possible exceptional points)

33.33% studentsanswered this correctly

Important Questions on Straight Line

HARD

Mathematics>Coordinate Geometry>Straight Line>Basics of 2D Coordinate Geometry

If a circle of radius

R

passes through the origin

O

and intersects the coordinate axes at

A

and

B

, then the locus of the foot of perpendicular from

O

A B

is :

MEDIUM

Mathematics>Coordinate Geometry>Straight Line>Basics of 2D Coordinate Geometry

Locus of the image of the point $(2, 3)$ in the line $(2 x - 3 y + 4) + k (x - 2 y + 3) = 0, k \in R,$ is a

EASY

Mathematics>Coordinate Geometry>Straight Line>Basics of 2D Coordinate Geometry

The coordinate of the point dividing internally the line joining the points

(4, - 2)

and

(8, 6)

in the ratio

7 : 5

MEDIUM

Mathematics>Coordinate Geometry>Straight Line>Basics of 2D Coordinate Geometry

Let

S

be the set of all triangles in the

x y

-plane, each having one vertex at the origin and the other two vertices lie on coordinate axes with integral coordinates. If each triangle in

S

has area

50

sq. units, then the number of elements in the set

S

is:

MEDIUM

Mathematics>Coordinate Geometry>Straight Line>Basics of 2D Coordinate Geometry

The locus of the point of intersection of the lines

\sqrt{2} x - y + 4 \sqrt{2} k = 0

and

\sqrt{2} k x + k y - 4 \sqrt{2} = 0

(

k

is any non-zero real parameter) is

EASY

Mathematics>Coordinate Geometry>Straight Line>Basics of 2D Coordinate Geometry

The area of a triangle is

5

sq units. Two of its vertices are

(2, 1)

and

(3, - 2)

.

The third vertex lies on

y = x + 3

,

then the coordinates of the third vertex can be

EASY

Mathematics>Coordinate Geometry>Straight Line>Basics of 2D Coordinate Geometry

(x, y)

is equidistant from

(a + b, b - a)

and

(a - b, a + b)

,

then

MEDIUM

Mathematics>Coordinate Geometry>Straight Line>Basics of 2D Coordinate Geometry

Consider a triangle

A B C

in the

x y

- plane with vertices

A = (0, 0), B = (1,1) a n d C = (9, 1)

. If the line

x = a

divides the triangle into two parts of equal area, then

a

equals

HARD

Mathematics>Coordinate Geometry>Straight Line>Basics of 2D Coordinate Geometry

In a circle with centre

O

, suppose

A, P, B

are three points on its circumference such that

P

is the mid-point of minor arc

A B

. Suppose when

∠ A O B = θ, \frac{a r e a (Δ A O B)}{a r e a (Δ A P B)} = \sqrt{5} + 2

∠ A O B

is doubled to

2 θ,

then the ratio

\frac{a r e a (Δ A O B)}{a r e a (Δ A P B)}

is.

HARD

Mathematics>Coordinate Geometry>Straight Line>Basics of 2D Coordinate Geometry

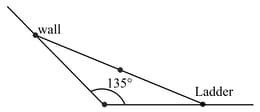
A wall is inclined to the floor at an angle of $135 ° .$ A ladder of length $l$ is resting on the wall. As the ladder slides down, its mid-point traces an arc of an ellipse. Then the area of the ellipse is
Question Image

EASY

Mathematics>Coordinate Geometry>Straight Line>Basics of 2D Coordinate Geometry

If the points

(2 a, a), (a, 2 a)

and

(a, a)

enclose a triangle of area

18

sq units, then the centroid of the triangle is equal to

MEDIUM

Mathematics>Coordinate Geometry>Straight Line>Basics of 2D Coordinate Geometry

Let

A = (a_{1}, a_{2})

and

B = (b_{1}, b_{2})

be two points in the plane with integer coordinates. Which one of the following is not a possible value of the distance between

A

and

B

HARD

Mathematics>Coordinate Geometry>Straight Line>Basics of 2D Coordinate Geometry

Let

A B C D

be a square of side length

1 .

Let

P, Q, R, S

be points in the interiors of the sides

A D, B C, A B, C D

respectively, such that

P Q

and

R S

intersect at right angles. If

P Q = \frac{3 \sqrt{3}}{4},

then

R S

equals

EASY

Mathematics>Coordinate Geometry>Straight Line>Basics of 2D Coordinate Geometry

The area of the triangle formed by the points

(a, b + c), (b, c + a), (c, a + b)

MEDIUM

Mathematics>Coordinate Geometry>Straight Line>Basics of 2D Coordinate Geometry

Let

A B C D

be a square of side length

1

, and

Γ

a circle passing through

B

and

C

, and touching

A D

. The radius of

Γ

MEDIUM

Mathematics>Coordinate Geometry>Straight Line>Basics of 2D Coordinate Geometry

If the sum of distances from a point

P

on two mutually perpendicular straight lines is

1

unit, then the locus of

P

MEDIUM

Mathematics>Coordinate Geometry>Straight Line>Basics of 2D Coordinate Geometry

Two line segments

A B

and

C D

are constrained to move along the

x

and

y

axes, respectively, in such a way that the points

A, B, C, D

are concyclic. If

A B = a a n d C D = b

, then the locus of the center of the circle passing through

A, B, C, D

in polar coordinates is

MEDIUM

Mathematics>Coordinate Geometry>Straight Line>Basics of 2D Coordinate Geometry

In a

∆ A B C

, medians,

A D

and

B E

are drawn. If

A D = 4

∠ D A B = \frac{π}{6} a n d ∠ A B E = \frac{π}{3}

, then the area of the

∆ A B C

EASY

Mathematics>Coordinate Geometry>Straight Line>Basics of 2D Coordinate Geometry

A B

is a straight line and

O

is point on the line

A B

. If one draws a line

O C

not coinciding with

O A

O B

, then the

∠ A O C

and

∠ B O C

are

MEDIUM

Mathematics>Coordinate Geometry>Straight Line>Basics of 2D Coordinate Geometry

A point

P

moves on the line

2 x - 3 y + 4 = 0 .

Q (1, 4)

and

R (3, - 2)

are fixed points, then the locus of the centroid of

Δ P Q R

is a line:

Let BC be a fixed line segment in the plane. The locus of a point A such that the triangle ABC is isosceles, is (with finitely many possible exceptional points)

Important Questions on Straight Line

Learn and Prepare for any exam you want !

Let $B C$ be a fixed line segment in the plane. The locus of a point $A$ such that the triangle $A B C$ is isosceles, is (with finitely many possible exceptional points)