MEDIUM

Earn 100

Locus of middle point of intercept of any tangent with respect to the circle $x^{2} + y^{2} = 4$ between the axis is

50% studentsanswered this correctly

Important Questions on Circle

MEDIUM

Mathematics>Geometry - II>Circle>Construct a tangent line from a point outside a given circle to the circle

P (- 9, - 1)

is a point on the circle

x^{2} + y^{2} + 4 x + 8 y - 38 = 0

, then find equation of the tangent drawn at the other end of the diameter drawn through

P

HARD

Mathematics>Geometry - II>Circle>Construct a tangent line from a point outside a given circle to the circle

Let

R S

be the diameter of the circle

x^{2} + y^{2} = 1

where,

S

is the point

(1, 0)

. Let

P

be a variable point (other than

R & S

) on the circle and tangents to the circle at

S & P

meet at the point

Q

. The normal to the circle at

P

intersects a line drawn through

Q

parallel to

R S

at point

E

. Then, the locus of

E

passes through the point (s):

EASY

Mathematics>Geometry - II>Circle>Construct a tangent line from a point outside a given circle to the circle

Find the equations of the tangents drawn to the circle

x^{2} + y^{2} = 50

at the points where the line

x + 7 = 0

meets it.

EASY

Mathematics>Geometry - II>Circle>Construct a tangent line from a point outside a given circle to the circle

The tangents of two points

A

and

B

on the circle with centre

O

intersect at a point

P .

If in quadrilateral

P A O B,

∠ A O B : ∠ A P B = 5 : 1,

then the measure of

∠ A P B

is given by

MEDIUM

Mathematics>Geometry - II>Circle>Construct a tangent line from a point outside a given circle to the circle

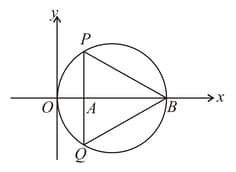
In the circle given below, let

O A = 1

unit,

O B = 13

unit and

P Q ⊥ O B

. Then, the area of the triangle

P Q B

(in square units) is :

Question Image

EASY

Mathematics>Geometry - II>Circle>Construct a tangent line from a point outside a given circle to the circle

Consider the circle

C

that passes through the points

(1, 0)

and

(0, 1)

having the smallest area. Then, the equation of the tangent to the circle

C

(0, 1)

EASY

Mathematics>Geometry - II>Circle>Construct a tangent line from a point outside a given circle to the circle

The area of a circle having the lines

3 x - 4 y + 4 = 0

and

6 x - 8 y - 7 = 0

as two of its tangents, is

HARD

Mathematics>Geometry - II>Circle>Construct a tangent line from a point outside a given circle to the circle

Find the equation of tangent and normal at

(3, 2)

of the circle

x^{2} + y^{2} - x - 3 y - 4 = 0

MEDIUM

Mathematics>Geometry - II>Circle>Construct a tangent line from a point outside a given circle to the circle

Let the normals at all the points on a given curve pass through a fixed point

(a, b)

. If the curve passes through

(3, - 3)

and

(4, - 2 \sqrt{2})

, given that

a - 2 \sqrt{2} b = 3

, then

(a^{2} + b^{2} + a b)

is equal to _____.

HARD

Mathematics>Geometry - II>Circle>Construct a tangent line from a point outside a given circle to the circle

Let the lengths of intercepts on

x

-axis and

y

-axis made by the circle

x^{2} + y^{2} + a x + 2 a y + c = 0,

(a < 0)

2 \sqrt{2}

and

2 \sqrt{5}

, respectively. Then the shortest distance from origin to a tangent to this circle which is perpendicular to the line

x + 2 y = 0,

is equal to :

EASY

Mathematics>Geometry - II>Circle>Construct a tangent line from a point outside a given circle to the circle

Tangents to a circle at points

P

and

Q

on the circle meet at a point

R

. If

P Q = 6

and

P R = 5

, then radius of the circle is

HARD

Mathematics>Geometry - II>Circle>Construct a tangent line from a point outside a given circle to the circle

If a tangent to the circle

x^{2} + y^{2} = 1

intersects the coordinate axes at distinct points

P

and

Q,

then the locus of the mid-point of

P Q

is:

MEDIUM

Mathematics>Geometry - II>Circle>Construct a tangent line from a point outside a given circle to the circle

If the angle between tangents drawn to

x^{2} + y^{2} + 2 g x + 2 f y + c = 0

from

(0, 0)

\frac{π}{2}

, then

EASY

Mathematics>Geometry - II>Circle>Construct a tangent line from a point outside a given circle to the circle

Which of the following lines is a normal to the circle

x^{2} + y^{2} - 2 x - 10 y + 6 = 0

MEDIUM

Mathematics>Geometry - II>Circle>Construct a tangent line from a point outside a given circle to the circle

Find the equation of the normal at

P (3, 5)

of the circle

S : x^{2} + y^{2} - 10 x - 2 y + 6

MEDIUM

Mathematics>Geometry - II>Circle>Construct a tangent line from a point outside a given circle to the circle

The radius of a circle, having minimum area, which touches the curve

y = 4 - x^{2}

and the lines,

y = |x|

is:

MEDIUM

Mathematics>Geometry - II>Circle>Construct a tangent line from a point outside a given circle to the circle

Find the area of the triangle formed by the tangent at

P (x_{1}, y_{1})

to the circle

x^{2} + y^{2} = a^{2}

with the coordinate axes where

x, y, \neq 0

MEDIUM

Mathematics>Geometry - II>Circle>Construct a tangent line from a point outside a given circle to the circle

Let

B

be the centre of the circle

x^{2} + y^{2} - 2 x + 4 y + 1 = 0 .

Let the tangents at two points

P

and

Q

on the circle intersect at the point

A (3, 1) .

Then

8 (\frac{area Δ APQ}{area Δ BPQ})

is equal to .

HARD

Mathematics>Geometry - II>Circle>Construct a tangent line from a point outside a given circle to the circle

Let

C

be the circle concentric with the circle,

2 x^{2} + 2 y^{2} - 6 x - 10 y = 183

and having area

{(\frac{1}{10})}^{th}

of the area of this circle. Then a tangent to

C,

parallel to the line,

3 x + y = 0

makes an intercept on the

y

-axis, which is equal to

MEDIUM

Mathematics>Geometry - II>Circle>Construct a tangent line from a point outside a given circle to the circle

Let the tangents drawn to the circle,

x^{2} + y^{2} = 16

from the point

P (0, h)

meet the

x

-axis at points

A

and

B

. If the area of

Δ A P B

is minimum, then positive value of

h

is:

Locus of middle point of intercept of any tangent with respect to the circle x2+y2=4 between the axis is

Important Questions on Circle

Learn and Prepare for any exam you want !

Locus of middle point of intercept of any tangent with respect to the circle $x^{2} + y^{2} = 4$ between the axis is