Match List I with List II:
List I
List II
(A)
Translational degrees of freedom
(I)
Monoatomic gases
(B)
Translational, rotational degrees of freedoms
(II)
Polyatomic gases
(C)
Translational, rotational and vibrational degrees of freedom
(III)
Rigid diatomic gases
(D)
Translational, rotational and more than one vibrational degrees of freedom
(IV)
Nonrigid diatomic gases
Choose the correct answer from the options given below:
Important Questions on Kinetic Theory of Gases and Radiation
Using equipartition of energy, the specific heat (in ) of Aluminium at high temperature can be estimated to be (atomic weight of Aluminium )
Match the ratio for ideal gases with different type of molecules:
| Molecule Type | |
| (A) Monoatomic | (I) |
| (B) Diatomic rigid molecules | (II) |
| (C) Diatomic non-rigid molecules | (III) |
| (D) Triatomic rigid molecules | (IV) |
Given below are two statements:
Statement I: In a diatomic molecule, the rotational energy at a given temperature obeys Maxwell's distribution.
Statement II : In a diatomic molecule, the rotational energy at a given temperature equals the translational kinetic energy for each molecule.
In the light of the above statements, choose the correct answer from the options given below:
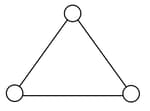
Consider a gas of triatomic molecules. The molecules are assumed to be triangular and made of massless rigid rods whose vertices are occupied by atoms. The internal energy of a mole of the gas at temperature T is:
(R-Universal gas constant)

