On pouring$10 \mathrm{g}$ mercury into a test tube of mass $8 g$ and external diameter $2 \mathrm{cm}$, the test tube floats vertically in the water. The test tube is pressed down into the water and left. Prove that the motion of the tube will be simple harmonic. Also find its time period.

a particle of mass m moves on the $X$-axis in a potential of the form $U\left(x\right)=k{x}^2$, it performs simple harmonic motion. The corresponding time period is proportional to $\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}$ as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of $\mathrm{x}=0$  in a way different from ${\mathrm{kx}}^2$ and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the $X$-axis. Its potential energy is $\mathrm{U}\left(\mathrm{x}\right)=\alpha x^4 (\mathrm{a}>0) \mathrm{for} \left|\mathrm{x}\right|$ near the origin and becomes a constant equal to ${\mathrm{U}}_0 \mathrm{for} \left|\mathrm{x}\right|>{\mathrm{x}}_0$(see figure below)

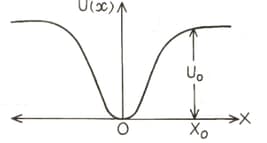
If the total energy of the particle is $\mathrm{E}$, it will perform periodic motion only if

A particle of mass m moves on the $X$-axis in a potential of the form $U\left(x\right)=k{x}^2$ , it performs simple harmonic motion. The corresponding time period is proportional to$\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}$, as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of $\mathrm{x}=0$  in a way different from ${\mathrm{kx}}^2$and its total energy is such that the particle does not escape to infinity. Consider a particle of mass $\mathrm{m}$ moving on the $X$-axis. Its potential energy is $\mathrm{U}\left(\mathrm{x}\right)=\alpha x^4(\alpha >0) \text{for} \left|\mathrm{x}\right|$ near the origin and becomes a constant equal to ${\mathrm{U}}_0\mathrm{for}\left|\mathrm{x}\right|>{\mathrm{x}}_0$(see figure below)

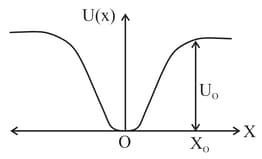
For periodic motion of small amplitude $\mathrm{A}$, the time period $\mathrm{T}$ of the particle is proportional to:

A particle of mass m moves on the X-axis in a potential of the form U (x) = k x, it performs simple harmonic motion. The corresponding time period is proportional to$\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}$ as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of $\mathrm{x}=0$  in a way different from ${\mathrm{kx}}^2$ and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the X-axis. Its potential energy is $\mathrm{U}\left(\mathrm{x}\right)={\mathrm{ax}}^4(\mathrm{a}>0) \mathrm{for} \left|\mathrm{x}\right|$ near the origin and becomes a constant equal to ${\mathrm{U}}_0 \mathrm{for} \left|\mathrm{x}>\right|>{\mathrm{x}}_0$ (see figure below)

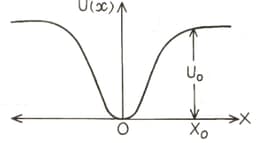
Acceleration of this particle for $\left|\mathrm{x}\right|>{\mathrm{x}}_0$  is 

Two SHM is represented by ${\mathrm{y}}_1=0.1 \sin \left[100\mathrm{\pi t}+\frac{\mathrm{\pi }}{3 }\right] \mathrm{and} {\mathrm{y}}_2=0.1 \cos \mathrm{\pi t}$. The phase difference of the velocity of particle $1$ with respect to $2$ is