Gamma Question Bank for Engineering Chemistry>Chapter -1 - Some Basic Concepts of Chemistry>Assignment>Q 27

EASY

JEE Main/Advanced

IMPORTANT

Earn 100

Out of following, which molecules has same weight under identical volume at STP?

12.5% studentsanswered this correctly

Important Points to Remember in Chapter -1 - Some Basic Concepts of Chemistry from Embibe Experts Gamma Question Bank for Engineering Chemistry Solutions

1. Matter and its Nature:

Based on their physical state and chemical characteristics, matter is classified as :

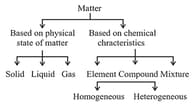
Question Image

These three states of matter are interconvertible by changing the conditions of temperature and pressure, i.e., they change their state.

${S o l i d}_{(ice)} \overset{H e a t}{\underset{C o o l}{⇌}} {L i q u i d}_{(Water)} \overset{H e a t}{\underset{C o o l}{⇌}} {G a s}_{(V a p o u r)}$

Based on the chemical composition, matter can be classified as:

(i) Element: Lavoisier $(1743 - 94)$ gave the explanation for element. According to him, an element consists of only one type of atoms. In different elements, atoms are different. The atoms of one element are different from the atoms of the other element. Thus, every element has its own independent property, which is not the same in other elements, e.g., carbon, sodium, oxygen etc.

(ii) Compound: When two or more elements combine chemically with one another, a compound is formed. When the compounds are formed, the elements present in them show new type of properties by losing their own individual properties. For example, hydrogen $(H)$ and oxygen $(O)$ are gases. Water $(H_{2} O)$ , formed by their combination, is a liquid. Here, hydrogen burns explosively in the air and oxygen is a supporter of combustion; but water is used as a fire extinguisher. Thus, hydrogen and oxygen change their properties in water.

(iii) Mixture: A mixture is a material consisting of two or more kinds of matter, each retaining its own characteristic property. A mixture can be separated by physical methods.

2. Measurement of Matter and the Uncertainty in Measurement:

(i) SI units (Basic units):

Physical quantity	Symbol for quantity	Symbol of SI units	Name of the unit
Length	$l$	$M$	Metre
Mass	$m$	$K g$	kilogram
Time	$t$	$S$	Second
Electric current	$I$	$A$	ampere
Thermodynamic temperature	$T$	$K$	Kelvin
Amount of substance	$n$	$m o l e$	mole
Luminous intensity	$I_{v}$	$C d$	candela

(ii) Prefixes used in the SI system:

Multiple	Prefix	Symbol
$10^{- 15}$	Femto	$f$
$10^{- 12}$	Pico	$p$
$10^{- 9}$	Nano	$n$
$10^{- 6}$	Micro	$μ$
$10^{- 3}$	Milli	$m$
$10^{- 2}$	Centi	$c$
$10^{- 1}$	Deci	$d$
$10$	Deca	$d a$
$10^{2}$	Hecta	$h$
$10^{3}$	Kilo	$k$
$10^{6}$	Mega	$M$
$10^{9}$	Giga	$G$
$10^{12}$	Tera	$T$
$10^{15}$	Peta	$P$

3. Significant Figures:

(i) There are three rules on determining how many significant figures are in a number:

(a) Non-zero digits are always significant.

(b) Any zeros between two significant digits are significant.

(c) A final zero or trailing zeros in the decimal portion only are significant.

(ii) The following rules dictate the way the numbers are to be rounded to the number of figures indicated:

(a) When rounding, examine the figure following (i.e., to the right of) the figure that is to be the last. This figure you are examining is the first figure to be dropped.

(b) If it is less than $5$ , drop it and all the figures to the right of it.

(c) If it is more than $5$ , increase by $1$ the number to be rounded, that is, the preceding figure.

(d) If it is $5$ , round the number so that it will be even. Keep in mind that zero is even when rounding off.

(iii) Addition and Subtraction with significant numbers:

For addition and subtraction, look at the decimal portion (i.e., to the right of the decimal point) of the numbers ONLY.

(a) Count the number of significant figures in the decimal portion of each number in the problem. (The digits to the left of the decimal place are not used to determine the number of decimal places in the final answer.)

(b) Add or subtract in the normal fashion.

(c) Round the answer to the LEAST number of places in the decimal portion of any number in the problem.

(iv) Multiplication and Division with significant numbers:

The LEAST number of significant figures in any number of the problem determines the number of significant figures in the answer.

4. Laws of Chemical Combinations:

The following are the laws which govern the formation of chemical compounds:

(i) Law of Conservation of Mass:

"Matter can neither be created nor destroyed." This law was put forth by Antoine Lavoisier in 1789.

(ii) Law of Constant Proportion:

"A given compound always contains exactly the same proportion of elements by weight."

Joseph Proust $(1754 - 1826)$ observed that samples of cupric carbonate obtained naturally and prepared synthetically in the laboratory had the same percentage composition of elements.

Cupric carbonate ${C u C O}_{3}$	$%$ of $C u$	$%$ of $C$	$%$ of $O$
Natural sample	$51.35$	$9.74$	$38.91$
Synthetic sample	$51.35$	$9.74$	$38.91$

(iii) Law of Multiple Proportion:

This law was proposed by Dalton in 1803. If two elements can combine to form more than one compound, the masses of one element that combine with a fixed mass of the other element are in the ratio of small whole number.

(iv) Gay Lussac’s Law of Gaseous Volumes:

This law was given by Gay Lussac in 1808. He observed that when gases combine or are produced in a chemical reaction, they do so in a simple ratio by volume, provided all gases are at the same temperature and pressure.

(v) Avogadro’s Law:

In $1811$ , Avogadro proposed that equal volumes of all gases at the same temperature and pressure should contain equal number of molecules. Avogadro made a distinction between atoms and molecules which is quite understandable in the present times.

5. Dalton’s Atomic Theory:

In $1808$ , Dalton published ‘A New System of Chemical Philosophy’, in which he proposed the following:

(i) Matter consists of indivisible atoms.

(ii) All atoms of a given element have identical properties, including identical mass. Atoms of different elements differ in mass.

(iii) Compounds are formed when atoms of different elements combine in a fixed ratio.

(iv) Chemical reactions involve reorganization of atoms. These are neither created nor destroyed in a chemical reaction.

Dalton’s theory could explain the laws of chemical combination.

6. Atomic and Molecular Mass:

(i) Atomic mass:

It is the average relative mass of its atoms as compared with an atom of carbon- $12$ isotope taken as $12$ .

The mass of $1$ atom $=$ atomic mass (in $a m u$ ).

The mass of $1$ mole atoms $=$ atomic mass (in $g$ ).

Example: The mass of one $O$ atom $= 16 a m u$ .

The mass of $1$ mole $O$ atoms $= 16 g$ .

(ii) Calculation of average atomic mass:

If an element exists in two isotopes having atomic masses ' $m_{1}$ and $m_{2}$ in the ratio $x : y$ , then:

Average atomic mass $= \frac{m_{1} \times x + m_{2} \times y}{x + y}$

(iii) Molecular mass:

Molecular mass of a substance is the average relative mass of its molecules as compared with an atom of $C$ -12 isotope taken as $12$ .

The mass of $1$ molecule $=$ molecular mass (in $a m u$ ).

The mass of $1$ mole molecules $=$ molecular mass (in $g$ ).

Example:

The mass of $1 O_{2}$ molecules $= 32 a m u$ .

The mass of $1 m o l O_{2}$ molecules $= 32 g m$ .

(a) For atom $\to 1 g$ atom $= 1$ mole.

For molecule $\to 1 g$ molecule $= 1$ mole.

(b) $1 a m u$ or $1 u = \frac{1}{12} t h$ of the mass of an atom of $C$ - $12 = 1.66 \times 10^{- 27} K g .$

(c) $M . W . = 2 (V a p o r D e n s i t y) .$

(d) $V a p o r D e n s i t y = \frac{d e n s i t y o f g a s}{d_{H_{2}}}$

(e) Atomic mass $\times$ Specific heat (in $c a l g m^{- 1}$ ) $\approx 6.4$ (Dulong-Petit law).

7. Mole Concept:

Moles can be calculated in following manner:

(i) Number of moles of molecules $= \frac{W e i g h t o f s u b s t a n c e (in g)}{M o l e c u l a r w e i g h t}$

(ii) Number of moles of atoms $= \frac{W e i g h t o f s u b s t a n c e (i n g)}{A t o m i c w e i g h t}$

(iii) Number of moles of gases $= \frac{V o l u m e o f g a s a t N . T . P . (i n l i t r e s)}{22.4 L}$

Mole of any gas occupies a volume of $22.4$ litres at $N . T . P .$ ,

( $N . T . P .$ corresponds to $0^{°} C$ and $1 a t m$ pressure).

(iv) Number of moles of atoms/molecules/ions $= \frac{\frac{N u m b e r o f \frac{a t o m s}{m o l e c u l e s}}{i o n s}}{A v o g a d r o c o n s t a n t}$

(Avogadro’s constant is equal to $6.022 \times 10^{23}$ ).

8. Empirical and Molecular Formula:

(i) Empirical formula of a compound is the simplest whole number ratio of the atoms of the elements constituting its one molecule. The sum of atomic masses of the atoms representing the empirical formula is called the empirical formula mass.

(ii) Molecular formula of a compound shows the actual number of the atoms of the elements present in its one molecule. The sum of atomic masses of the atoms representing the molecule is called the molecular mass.

(iii) Relationship between the empirical formula and the molecular formula.

Molecular formula = $n \times$ empirical formula, where $n$ is a simple whole number having values of $1,2, 3 \dots$ , etc.

Also, $n =$ Molecular formula mass/Empirical formula mass.

Question Image

9. Percentage Composition of Compounds:

Percentage Composition of Element:

When a compound is formed from two or more elements, the amount of the element present in a compound is always proportional to its definite mass.

Mass $%$ of an element $= \frac{M a s s o f t h e e l e m e n t i n t h e c o m p o u n d \times 100}{M o l a r m a s s o f t h e c o m p o u n d .}$

Example:

Calculate the percentage of both the elements present in water $(H_{2} O)$ .

Solution:

Atomic mass of $H = 1.0 g r a m {m o l e}^{- 1}$ .

Atomic mass of $O = 16.0 g r a m {m o l e}^{- 1}$ .

Molecular mass of $H_{2} O = 18.0 g r a m {m o l e}^{- 1}$ .

Mass $%$ of Hydrogen $= \frac{2 (1.0 g {m o l}^{- 1}) \times 100}{18.0 g {m o l}^{- 1}}$

$= 11.11 %$ .

Mass $%$ of Oxygen $= \frac{(16.0 g {m o l}^{- 1}) \times 100}{18.0 g {m o l}^{- 1}}$

$= 88.89 %$ .

10. Chemical Equations and Stoichiometry:

A chemical reaction can be expressed in the form of a chemical equation from which we obtain a large amount of qualitative and quantitative information. Quantitative information is available from the balanced chemical equation available from the stoichiometry of a given reaction. A balanced equation for combustion of methane is given below. Let us consider what information is available from stoichiometry.

${C H}_{4 (g)} + 2 O_{2 (g)} \to {C O}_{2 (g)} + 2 H_{2} O_{(g)}$

	${C H}_{4}$	$O_{2}$	${C O}_{2}$	$H_{2} O$
Mole	$1$ mole	$2$ mole	$1$ mole	$2$ mole
Molecules	$1$ molecule	$2$ molecule	$1$ molecule	$2$ molecule
Volume at N.T.P.	$22.4 L$	$2 \times 22.4 = 44.8 L$	$22.4 L$	$2 \times 22.4 = 44.8 L$
Mass	$16.00 g$	$2 \times 32 = 64 g$	$44.00 g$	$2 \times 18 = 36 g$
Number of molecules	$6.022 \times 10^{23}$	$2 \times 6.022 \times 10^{23}$	$6.022 \times 10^{23}$	$2 \times 6.022 \times 10^{23}$

The stoichiometry of the reactants in the above reaction is $1 : 2$ and the stoichiometry of the product is also $1 : 2$ . Thus, for a general reaction, $a A + b B \to c C + d D$ , the stoichiometries of the reactants and the products are $a : b$ and $c : d$ , respectively.

11. Limiting Reagent:

In the given reaction, if number of quantities (either in $g m$ /mole/molecules) are present with exact coefficients, the chemical reaction goes to completion without any reactant left unused.

However, if the exact proportion is not present, the one which gets totally consumed is known as the limiting reagent (Limiting reagent decides the product quantity for the given information).

Example: $2 H_{2} + O_{2} \to 2 H_{2} O$

In the above e.g., $2$ moles of $H_{2}$ react exactly with $1$ mole of $O_{2}$ to give $2$ moles of $H_{2} O$ . If the given moles of $H_{2}$ are $4$ moles and that of $O_{2}$ are $0.5$ , $0.5$ moles $O_{2}$ will act as a limiting reagent as it is in the minimum amount and the product formation is given w.r.t. $O_{2}$ , i.e., $1$ mole of $H_{2} O$ .

Percentage Yield

Percentage yield of a reaction $= \frac{a c t u a l a m o u n t o f p r o d u c t o b t a i n e d}{t h e o r e t i c a l a m o u n t o f p r o d u c t} \times 100$ .

12. Concentration Terms:

(i) Molarity $(M)$ :

It is the number of moles of the solute present per litre of the solution.

$M = \frac{n}{V} = \frac{W}{M_{w} V_{i n l i t r e}} = \frac{W}{M_{w}} \frac{1000}{V_{i n c c}}$

$M \times V_{i n c c} = \frac{W}{M_{w}} 1000$

$\Rightarrow M \times V (m l) =$ millimoles

The molarity changes with the temperature of the solution. Increase in the temperature generally decreases the molarity. It is the most convenient method to express the concentration of the solution. On dilution, the molarity decreases.

(ii) Molality $(m)$ :

Number of moles $(n)$ of the solute present per $k g$ of the solvent.

$m = \frac{n}{W_{i n k g}} = \frac{W}{M W_{i n k g}} = \frac{W}{M {W_{i n g}}_{s o l v e n t}} 1000$

It is independent of the temperature since no volume factor is involved in the equation.

(iii) Mole fraction $(X) :$

It is the ratio of the number of moles of one component to the total number of moles present in the solution.

For a system having two components $A$ and $B$ ,

$X_{A} = \frac{n_{A}}{n_{A} + n_{B}}, X_{B} = \frac{n_{B}}{n_{A} + n_{B}}$

$X_{A} + X_{B} = 1$ .

The mole fraction is also independent of the temperature.

(iv) In terms of $%$ composition:

$%$ by weight $= \frac{W t . o f s o l u t e}{W t . o f s o l u t i o n} \times 100$ .

$%$ weight by volume $= \frac{W t . o f s o l u t e}{V o l . o f s o l u t i o n} \times 100$ (In case of a solid dissolved in a liquid).

$%$ by volume $= \frac{V o l u m e o f s o l u t e}{V o l u m e o f s o l u t i o n} \times 100$ (In case of a liquid dissolved in another liquid).

$P P M = \frac{N o . o f p a r t s o f s o l u t e}{N o . o f p a r t s o f s o l u t i o n} \times 10^{6}$ .

$%$ by weight is independent of the temperature, while $%$ by volume is temperature dependent.

13. Miscellaneous Conversions:

(i) Mole fraction of the solute into molarity of the solution $M = \frac{x_{2} ρ \times 1000}{x_{1} M_{1} + M_{2} x_{2}}$ .

(ii) Molarity into the mole fraction $x_{2} = \frac{{M M}_{1} \times 1000}{ρ \times 1000 - {M M}_{2}}$ .

(iii) Mole fraction into the molality $m = \frac{x_{2} \times 1000}{x_{1} M_{1}}$ .

(iv) Molality into the mole fraction $x_{2} = \frac{m M_{1}}{1000 + m M_{1}}$ .

(v) Molality into the molarity $M = \frac{m ρ \times 1000}{1000 + {m M}_{2}}$ .

(vi) Molarity into the molality $m = \frac{M \times 1000}{1000 ρ - {M M}_{2}}$ .

$M_{1}$ and $M_{2}$ are the molar masses of the solvent and the solute, $ρ$ is the density of the solution $(g m {m L}^{- 1})$ , $M =$ Molarity $(m o l e l i t^{- 1})$ , $m =$ Molality $(m o l e k g^{- 1})$ , $x_{1} =$ Mole fraction of the solvent, $x_{2} =$ Mole fraction of the solute.

Learn and Prepare for any exam you want !

|

|

|

|

|

|

|

|