MEDIUM
9th ICSE
IMPORTANT
Earn 100
Perpendiculars are drawn from a point within an equilateral triangle to the three sides. Prove that the sum of the three perpendiculars is equal to the altitude of the triangle.

Important Questions on Theorems on Area
HARD
9th ICSE
IMPORTANT
HARD
9th ICSE
IMPORTANT
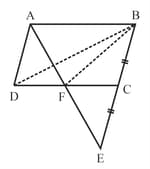
In the adjoining figure, is a parallelogram in which is produced to such that . intersects . If area of , find the area of parallelogram .
HARD
9th ICSE
IMPORTANT
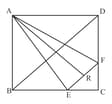
is a square. and are respectively the midpoints of and . If is the mid-point of as shown in the figure, prove that .
MEDIUM
9th ICSE
IMPORTANT
In the figure and are the midpoints of and respectively, and and BXP is straight lines. Prove that .