Position (in ) of a particle moving on a straight line varies with time (in ) as . Consider the motion of the particle from to . Here, is the total distance travelled and is the distance travelled during retardation. Find .

Important Questions on Kinematics
Two particles are thrown from the top of a tower with the same speed in upward and downward directions simultaneously. If the first particle hits the ground in time and the second particle takes time after the first one hitting the ground to hit the ground. Then find
Maximum height attained by the second particle above the tower.
Height of tower
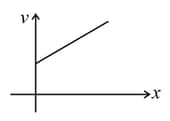
A particle moves along -axis in a positive direction. Its acceleration is given as , where denotes the -coordinate of particle, and are positive constants. For velocity-position graph of particle to be of type as shown in figure, find the value of speed (in ) of particle at . Take and
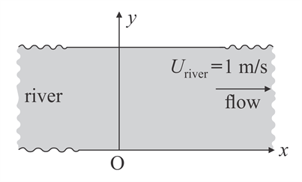
A man can swim in still water with a speed of , and -axes are drawn along and normal to the bank of river flowing to right with a speed of . The man starts swimming from origin at second. Assume the size of the man to be negligible. Find the equation of locus of all the possible points where the man can reach at .
Two swimmers , one located on one side and other on the another side of a river, are situated at a distance from each other. The line joining them is making an angle with the direction perpendicular to the flow. The speed of each swimmer with respect to still water is and speed of river flow is . Both start swimming at the same time in the direction parallel to line towards each other and they keep on swimming in the same direction. Then,
(a) Find the time after which they meet.
(b) Find the speed of river so that the path of the two swimmers with respect to the ground becomes perpendicular to each other.
Two particles start simultaneously from the same point and move along two straight lines making an angle with each other. One move with uniform velocity and the other with constant acceleration and initial velocity zero.
(a) Find the least relative velocity of one with respect to the other.
(b) At the same time, find the distance between the two particles.
