Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.

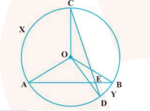
If two chords $AB$and $CD$ of a circle $AYDZBWCX$intersect at right angles as shown in the figure, prove that $\mathrm{arc}$ $\mathrm{CXA}+$ $\mathrm{arc}$$\text{DZB}=\mathrm{arc} \text{AYD}+\mathrm{arc} \text{BWC}=$semicircle.

In the given fig., $AB$ and $CD$ are two chords of a circle intersecting each other at point $E$. Prove that $\angle AEC=\frac{1}{2}$ (Angles subtended by an $\text{arc CXA}$ at the centre $+$ angle subtended by arc $DYB$ at the centre.)

A circle has radius $\sqrt{2 }\mathrm{cm}.$ It is divided into two segments by a chord of length $2 \mathrm{cm}.$

Prove that the angle subtended by the chord at a point in major segment is ${45}^o$.

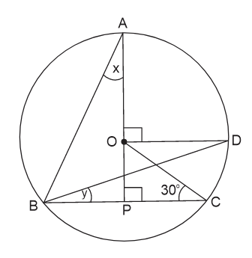
In Fig. $10.20$, $O$ is the centre of the circle, $\angle BCO={30}^o$. Find $x$ and $y$.