In given figure, ∠ A C B = 90 ° and C D ⊥ A B , prove that C D 2 = B D × A D

Given, in ∆ A B C , ∠ A C B = 90 ° and C D ⊥ A B . To prove: C D 2 = B D × A D Proof: In ∆ C A D , C A 2 = C D 2 + A D 2 ------------(i) Similarly, In ∆ C D B , C B 2 = C D 2 + B D 2 -------(ii) Adding (i) and (ii), we get, C A 2 + C B 2 = C D 2 + A D 2 + C D 2 + B D 2 ⇒ A B 2 = 2 C D 2 + A D 2 + B D 2 ⇒ A B 2 - A D 2 = B D 2 + 2 C D 2 ⇒ A B + A D A B - A D - B D 2 = 2 C D 2 ⇒ A B + A D B D - B D 2 = 2 C D 2 ⇒ B D A B + A D - B D = 2 C D 2 ⇒ B D A B - B D + A D = 2 C D 2 ⇒ B D × 2 A D = 2 C D 2 ⇒ C D 2 = B D × A D Hence, proved.

In an equilateral △ A B C , D is a point on side B C , such that B D = 1 3 B C . Prove that 9 A D 2 = 7 A B 2 .

Given: An equilateral △ A B C , D is a point on B C such that B D = 1 3 B C To Prove: 9 A D 2 = 7 A B 2 Construction: Draw A P ⊥ B C . Proof: We have B D = 1 3 B C = 1 3 A B Since △ A B C is an equilateral and A P ⊥ B C B P = P C = 1 2 B C = 1 2 A B Using Pythagoras theorem in △ A B P , A P 2 + B P 2 = A B 2 A P 2 = A B 2 - B P 2 = A B 2 - A B 2 2 = 3 4 A B 2 --[1] Using Pythagoras theorem in △ A D P , A D 2 = A P 2 + D P 2 A D 2 = 3 4 A B 2 + B P - B D 2 A D 2 = 3 4 A B 2 + 1 2 A B - 1 3 A B 2 A D 2 = 3 4 A B 2 + 1 36 A B 2 A D 2 = 27 A B 2 + A B 2 36 A D 2 = 28 36 A B 2 A D 2 = 7 9 A B 2 9 A D 2 = 7 A B 2 Hence Proved.

HARD

Earn 100

Prove that the area of the semicircle drawn on the hypotenuse of a rightangled triangle is equal to the sumof the areas of the semicircles drawn on the other two sides of the triangle.

Important Questions on Geometry

HARD

Mathematics>Geometry>Geometry>Explain a proof of the Pythagorean Theorem and its converse.

Triangles

A B C

and

D E F

are such that

∠ A = ∠ D, A B = D E = 17, B C = E F = 10

and

A C - D F = 12

. What is

A C + D F

MEDIUM

Mathematics>Geometry>Geometry>Explain a proof of the Pythagorean Theorem and its converse.

Triangle

P Q R

is a right-angled at

Q

. If

P Q = 6 cm

P R = 10 cm

, then

Q R

is equal to:

HARD

Mathematics>Geometry>Geometry>Explain a proof of the Pythagorean Theorem and its converse.

A village has a circular wall around it, and the wall has four gates pointing north, south, east and west. A tree stands outside the village,

16 m

north of the north gate, and it can be just seen appearing on the horizon from a point

48 m

east of the south gate. What is the diameter, in meters, of the wall that surrounds the village?

HARD

Mathematics>Geometry>Geometry>Explain a proof of the Pythagorean Theorem and its converse.

A semicircular paper is folded along a chord such that the folded circular arc is tangent to the diameter of the semicircle. The radius of the semicircle is $4$ units and the point of tangency divides the diameter in the ratio $7 : 1 .$ If the length of the crease (the dotted line segment in the figure) is $l$ then determine $l^{2} .$

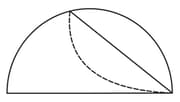
Question Image

MEDIUM

Mathematics>Geometry>Geometry>Explain a proof of the Pythagorean Theorem and its converse.

Six consecutive sides of an equiangular octagon are

6, 9, 8, 7, 10, 5

in that order. The integer nearest to the sum of the remaining two sides is

MEDIUM

Mathematics>Geometry>Geometry>Explain a proof of the Pythagorean Theorem and its converse.

A friction-less board has the shape of an equilateral triangle of side length

1

meter with bouncing walls along the sides. A tiny super bouncy ball is fired from vertex

A

towards the side

B C .

The ball bounces off the walls of the board nine times before it hits a vertex for the first time. The bounces are such that the angle of incidence equals the angle of reflection. The distance travelled by the ball in meters is of the form

\sqrt{N},

where

N

is an integer. What is the value of

N ?

EASY

Mathematics>Geometry>Geometry>Explain a proof of the Pythagorean Theorem and its converse.

A ladder leaning against a wall makes an angle

θ

with the horizontal ground such that

\cos (θ) = \frac{5}{13}

. If the height of the top of the ladder from the wall is

18 m

, then what is the distance (in

m

) of the foot of the ladder from the wall?

HARD

Mathematics>Geometry>Geometry>Explain a proof of the Pythagorean Theorem and its converse.

Prove that, in a right triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.

MEDIUM

Mathematics>Geometry>Geometry>Explain a proof of the Pythagorean Theorem and its converse.

From an external point

P

, a tangent

PQ

is drawn to a circle, with the centre

O

,touching the circle at

Q

. If the distance of

P

from the centre is

13 cm

and length of tangent

PQ

12 cm

, then the radius of the circle is

HARD

Mathematics>Geometry>Geometry>Explain a proof of the Pythagorean Theorem and its converse.

∆ A B C, ∠ B = 90 °

. If points

D

and

E

are on the side

B C

such that

B D = D E = E C

, then which of the following is true?

EASY

Mathematics>Geometry>Geometry>Explain a proof of the Pythagorean Theorem and its converse.

P

and

Q

are the points on side

C A

and

C B

respectively of triangle

△ A B C

, right angled at

C

, prove that

(A Q^{2} + B P^{2}) = (A B^{2} + P Q^{2})

HARD

Mathematics>Geometry>Geometry>Explain a proof of the Pythagorean Theorem and its converse.

A very tall tree breaks from the middle due to storm. The broken part of the tree did not separate from the tree and the top of the tree touched the ground at a distance of

12

metre from the base of the tree. If the tree broke at the height of

37

metre from the ground, then what is the length of the broken portion of the tree in metres?

EASY

Mathematics>Geometry>Geometry>Explain a proof of the Pythagorean Theorem and its converse.

Prove that in a right angle triangle, the square of the hypotenuse is equal the sum of squares of the other two sides.

EASY

Mathematics>Geometry>Geometry>Explain a proof of the Pythagorean Theorem and its converse.

Let

a b c

be a three-digit number with nonzero digits such that

a^{2} + b^{2} = c^{2}

. What is the largest possible prime factor of

\bar{a b c} ?

MEDIUM

Mathematics>Geometry>Geometry>Explain a proof of the Pythagorean Theorem and its converse.

In given figure,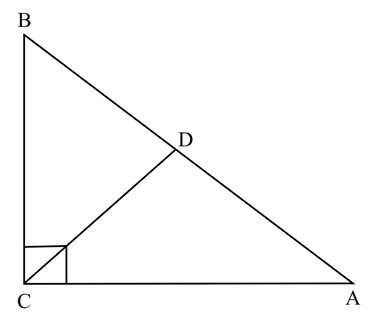 Question Image

$∠ A C B = 90 °$ and $C D ⊥ A B$ , prove that $C D^{2} = B D \times A D$

MEDIUM

Mathematics>Geometry>Geometry>Explain a proof of the Pythagorean Theorem and its converse.

In a triangle, if square of one side is equal to the sum of the squares of the other two sides, then prove that the angle opposite to its first side is a right angle.

HARD

Mathematics>Geometry>Geometry>Explain a proof of the Pythagorean Theorem and its converse.

In an equilateral

△ A B C

D

is a point on side

B C

, such that

B D = \frac{1}{3} B C

. Prove that

9 A D^{2} = 7 A B^{2}

MEDIUM

Mathematics>Geometry>Geometry>Explain a proof of the Pythagorean Theorem and its converse.

△ ABC, ∠ C = 90 °, AC = 5 cm

and

BC = 12 cm

. The bisector of

∠ A

meets

BC

D

. What is the length of

AD

?

HARD

Mathematics>Geometry>Geometry>Explain a proof of the Pythagorean Theorem and its converse.

Let

P Q R

be a triangle in which

P Q = 3

. From the vertex

R,

draw the altitude

R S

to meet

P Q

S

. Assume that

R S = \sqrt{3}

and

P S = Q R

. Then,

P R

equals

EASY

Mathematics>Geometry>Geometry>Explain a proof of the Pythagorean Theorem and its converse.

The circle of radius

4 c m

and centre

O

has a tangent

P R

. If

∠ P O R = 90^{o}

and

O R = 7 c m

and

O P = 24 c m

. Calculate the length (in

c m

.) of

P R

Prove that the area of the semicircle drawn on the hypotenuse of a rightangled triangle is equal to the sumof the areas of the semicircles drawn on the other two sides of the triangle.

Important Questions on Geometry

Learn and Prepare for any exam you want !