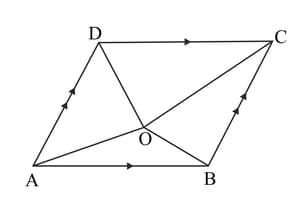
Prove that the diagonals of a parallelogram divide it into four triangle of equal are.

Important Questions on Theorems on Area
In the figure given below, is the median of triangle and is any point on . Prove that the area of the triangle the area of triangle .
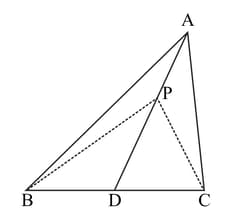
In the figure given below, is the median of triangle and is any point on . Prove that the area of the triangle the area of triangle .
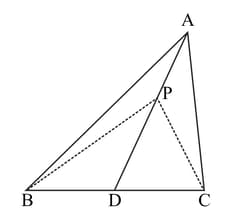
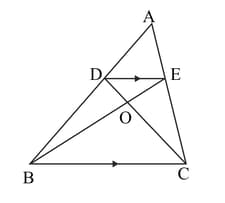
In the figure given below, , prove that the area of the triangle area of the triangle .
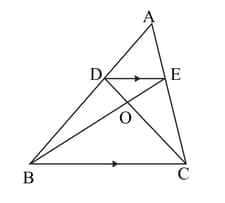
In the figure given below, , prove that the area of the triangle area of the triangle .
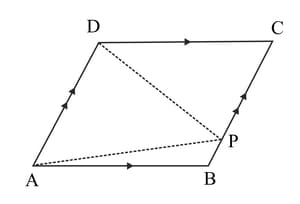
In the figure given below, is parallelogram and is any point in . Prove that the area of triangle the area of triangle area of triangle .
In the figure given below, is any point inside a parallelogram . Prove that area of area of area of .
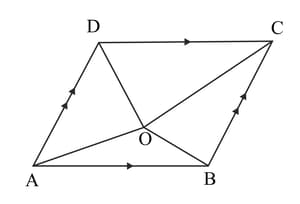
In the figure given below, is any point inside a parallelogram . Prove that area of area of area of .