HARD
Earn 100
Prove that the ratio of areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Important Questions on Theorems regarding Similarity
MEDIUM
MEDIUM
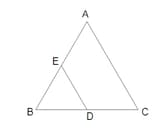
MEDIUM
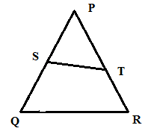
EASY
HARD
Let be a triangle and be a point on side closer to vertex than . Let be a point on side such that is parallel to and let be a point on side such that is parallel to . If the area of the quadrilateral is equal to of the area of , then the ratio equals
EASY
In the given figure, if and , then the measure of is:
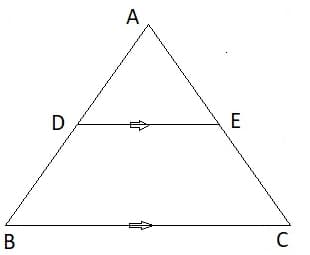
HARD
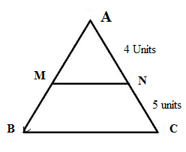
EASY
MEDIUM
MEDIUM
MEDIUM
HARD
EASY
EASY
MEDIUM
EASY
HARD
EASY
Consider the following figure shown below and choose which of the following equation is CORRECT about the similarity of both triangles?
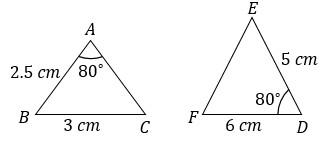
HARD
HARD
In a triangle with points are on the interior of segments respectively. Which of the following triangles cannot be similar to the triangle ?

