Gamma Question Bank for Engineering Chemistry>Chapter -1 - The Solid State>Assignment Set-2>Q 1

MEDIUM

JEE Main/Advanced

IMPORTANT

Earn 100

Quartz on strong heating followed by rapid cooling gives glass which is an amorphous solid because

57.14% studentsanswered this correctly

Important Points to Remember in Chapter -1 - The Solid State from Embibe Experts Gamma Question Bank for Engineering Chemistry Solutions

1. Classification and Properties of Solids:

The following are the characteristic properties of the solid state:

(i) They have definite mass, volume, and shape.

(ii) Intermolecular distances are short.

(iii) Intermolecular forces are strong.

(iv) Their constituent particles (atoms, molecules, or ions) have fixed positions and can only oscillate about their mean positions.

(v) They are incompressible and rigid.

Amorphous and Crystalline solids:

Property	Crystalline solids	Amorphous solids
Shape	Definite characteristic geometrical shape	Irregular shape
Melting point	Melt at a sharp and characteristic temperature	Gradually soften over a range of temperature
Cleavage property	When cut with a sharp-edged tool, they split into two pieces and the newly generated surfaces are plain and smooth	When cut with a sharp-edged tool, they cut into two pieces with irregular surfaces
Heat of fusion	They have a definite and characteristic heat of fusion	They do not have definite heat of fusion
Anisotropy	Anisotropic in nature	Isotropic in nature
Nature	True solid	Pseudo solids or super cooled liquids
Order in arrangement of constituent particles	Long range order	Only short-range order.

Classification of Crystalline Solids and their Properties:

	Type of Solid	Constituent Particles	Bonding/ Attractive Forces	Examples	Physical Nature	Electrical Conductivity	Melting Point
(1)	Molecular solids	Molecules
	(i) Nonpolar		Dispersion or London forces	$A r, {C C l}_{4}, H_{2},$ $I_{2}, {C O}_{2}$	Soft	Insulator	Very low
	(ii) Polar		Dipole-dipole interactions	$H C l, {S O}_{2}$	Soft	Insulator	Low
	(iii) Hydrogen bonded		Hydrogen bonding	$H_{2} O (i c e)$	Hard	Insulator	Low
(2)	Ionic solids	Ions	Coulombic or electrostatic	$N a C l, M g O,$ $Z n S, {C a F}_{2}$	Hard but brittle	Insulators in solid state but conductors in molten state and in aqueous solutions	High
(3)	Metallic solids	Positive ions in a sea of delocalised electrons	Metallic bonding	$F e, C u, A u,$ $M g$	Hard but Malleable and ductile	Conductors in solid state as well as in molten state	Fairly high
(4)	Covalent or network solids	Atoms	Covalent bonding	${S i O}_{2}$ (quartz), $S i C$ , $C$ (diamond), $A l N$	Hard	Insulators	Extremely high
				$C_{(g r a p h i t e)}$	Soft	Conductor (exception)

2. Crystal Lattice and Unit Cells:

A regular three-dimensional arrangement of points in space is called a crystal lattice. There are only $14$ possible three-dimensional lattices. These are called Bravais Lattices (after the French mathematician who first described them). The following are the characteristics of a crystal lattice:

(i) each point in a lattice is called lattice point or lattice site.

(ii) each point in a crystal lattice represents one constituent particle which may be an atom, a molecule (a group of atoms) or an ion.

(iii) lattice points are joined by straight lines to bring out the geometry of the lattice.

Unit cell is the smallest portion of a crystal lattice which, when repeated in different directions, generates the entire lattice. A unit cell is characterised by:

(a) its dimensions along with the three edges, $a, b$ and $c$ . These edges may or may not be mutually perpendicular.

(b) angles between the edges, $α$ (between $b$ and $c$ ) $β$ (between $a$ and $c$ ) and $γ$ (between $a$ and $b$ ). Thus, a unit cell is characterised by six parameters, $a, b, c, α, β$ and $γ$ .

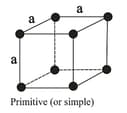
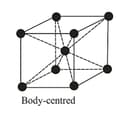
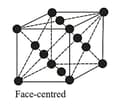
Seven Primitive Unit Cells and their Possible Variations as Centred Unit Cells

Crystal system	Possible variations	Axial distances or edge lengths	Axial angles	Examples
Cubic	Primitive, Body-centred, Face-centred	$a = b = c$	$α = β = γ = 90^{\circ}$	$N a C l$ , Zinc bland, $C u$
Tetragonal	Primitive, Body-centred	$a = b \neq c$	$α = β = γ = 90^{\circ}$	White tin, $S n O_{2}, {T i O}_{2}, {C a S O}_{4}$
Orthorhombic	Primitive, Body-centred, Face-centred, End-centred	$a \neq b \neq c$	$α = β = γ = 90^{\circ}$	Rhombic sulphur, ${K N O}_{3}, {B a S O}_{4}$
Hexagonal	Primitive	$a = b \neq c$	$α = β = 90^{\circ}$ , $γ = 120^{\circ}$	Graphite, $Z n O, C d S$
Rhombohedral or Trigonal	Primitive	$a = b = c$	$α = β = γ \neq 90^{\circ}$	Calcite $({C a C O}_{3})$ , $H g S$ (cinnabar)
Monoclinic	Primitive, End-centred	$a \neq b \neq c$	$α = γ = 90^{\circ}$ , $β \neq 90^{\circ}$	Monoclinic sulphur, ${N a}_{2} {S O}_{4} \cdot 1 {0 H}_{2} O$
Triclinic	Primitive	$a \neq b \neq c$	$α \neq β \neq γ \neq 90^{\circ}$	$K_{2} {C r}_{2} O_{7}, {C u S O}_{4} . 5 H_{2} O,$ $H_{3} {B O}_{3}$

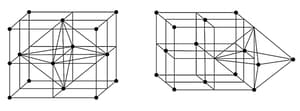
The three cubic lattices: all sides are of same length, and angles between the faces are $90^{\circ}$

3. Calculations for Standard Cubical Unit Lattice:

Geometry of a cube	Contribution of atom at different sites of cube
Number of comers $= 8$	at corner $= \frac{1}{8}$
Number of faces $= 6$	at face $= \frac{1}{2}$
Number of edges $= 12$	at edge $= \frac{1}{4}$
Number of body centre $= 1$	at body centre $= 1$
Number of body diagonals $= 4$
Number of face diagonals $= 12$
Number of face centres $= 6$
Number of edge centres $= 12$

	Simple Cubic Cell $(S C C)$	Body centred Cubic Cell $(B C C)$ ( $S C C +$ Body centred $= B C C$ )	Face centred Cubic Cell $(F C C)$ ( $S C C +$ Face centred $= F C C$ )
Geometry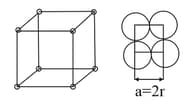
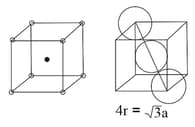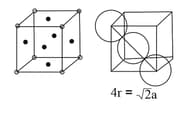Number of atoms per unit cell $(n)$	$= 8 \times \frac{1}{8} = 1$ corners	$= \underset{c o r n e r}{(8 \times \frac{1}{8})} + \underset{b o d y c e n t r e}{(1 \times 1) = 2}$	$= \underset{c o r n e r}{(8 \times \frac{1}{8})} + \underset{f a c e c e n t r e}{(6 \times \frac{1}{2}) = 4}$
Coordination no.	$6$	$8$	$12$
Relation between $a$ and $r$	$a = 2 r$	$4 r = \sqrt{3} a$	$4 r = \sqrt{2} a$
Packing efficiency $P . E . = \frac{n \times \frac{4}{3 π r^{3}}}{a^{3}}$	$\frac{π}{6}$ or $52.4 %$	$\frac{\sqrt{3} π}{8}$ or $68 %$	$\frac{π}{3 \sqrt{2}}$ or $74 %$

Density of the unit cell $= \frac{n \times M}{V \times N_{A}} {g c m}^{- 3}$

Where $M =$ Molecular weight or atomic weight

4. Neighbourhood of a Particle:

(i) Simple Cubic $(S C)$ Structure:

Type of neighbour	Distance	No. of neighbours
First nearest	$a$	$6$ (shared by $4$ cubes)
Second nearest	$a \sqrt{2}$	$12$ (shared by $2$ cubes)
Third nearest	$a \sqrt{3}$	$8$ (unshared)

(ii) Body Centred Cubic $(B C C)$ Structure:

Type of neighbour	Distance	No. of neighbours
First nearest	$2 r = a \frac{\sqrt{3}}{2}$	$8$
Second nearest	$= a$	$6$
Third nearest	$a \sqrt{2}$	$12$
Fourth nearest	$= a \frac{\sqrt{11}}{2}$	$24$
Fifth nearest	$a \sqrt{3}$	$8$

(iii) Face Centred Cubic $(F C C)$ Structure:

Type of neighbour	Distance	No. of neighbours
First nearest	$\frac{a}{\sqrt{2}}$	$12 = (\frac{3 \times 8}{2})$
Second nearest	$a$	$6 = (\frac{3 \times 8}{4})$
Third nearest	$a \sqrt{\frac{3}{2}}$	$24$
Fourth nearest	$a \sqrt{2}$	$12$
Fifth nearest	$a \sqrt{\frac{5}{2}}$	$24$

5. Packing in Solids:

(i) Three-dimensional close packing

Contents	$B C C$	$CCP / FCC$	$H C P$
Type of packing	$A B A B \dots \dots \dots \dots \dots$ Packing but not close packing	$A B C A B C \dots \dots \dots$ close packing	$A B A B \dots \dots \dots \dots \dots$ close packing
No. of atoms	$2$	$4$	$6$
Coordination No.	$8$	$12$	$12$
Packing efficiency	$68 %$	$74 %$	$74 %$
Examples	$IA$ group, $Ba$ , $F e$	$C a, S r, A l$ , $C o$ group, $N i$ group, Copper group, all inert gases except helium	Remaining $d$ -block elements $B e & M g$

Note: Only $M n$ crystallises in $S . C . C .$

6. Voids:

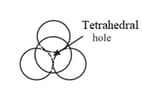
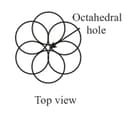
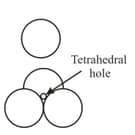
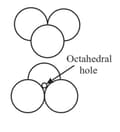
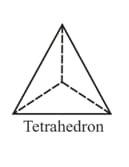
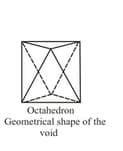
Tetrahedral and octahedral voids

Question Image

top view

Question Image

exploded side view

Question Image

geometrical shape of the void.

The number of these two types of voids depend upon the number of close packed spheres. Let the number of close packed spheres be $N$ , then:

The number of octahedral voids generated $= N$

The number of tetrahedral voids generated $= 2 N$

7. Locating Tetrahedral and Octahedral Voids in $F C C$ Lattice:

(i) Tetrahedral voids:

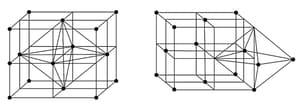
Let us consider a unit cell of $c c p$ or $f c c$ lattice is divided into eight small cubes. Each small cube has atoms at alternate corners. In all, each small cube has $4$ atoms. When joined to each other, they make a regular tetrahedron. Thus, there is one tetrahedral void in each small cube and eight tetrahedral voids in total.


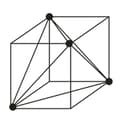Eight tetrahedral voids per unit cell of $c c p$ structure	one tetrahedral void showing the geometry.

(ii) Octahedral voids:

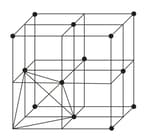
(a) $c c p$ or $f c c$ lattice has one octahedral void at the body centre of the cube.

(b) Besides the body centre, there is one octahedral void at the centre of each of the $12$ edges. Since each edge of the cube is shared between four adjacent unit cells, so as the octahedral void located on it. Therefor only ${(¼)}^{t h}$ of each void belongs to a particular unit cell.

Location of octahedral voids per unit cell of $c c p$ or $f c c$ lattice
at the body centre of the cube	at the centre of each edge (only one such void is shown)

Question Image

at the body centre of the cube

Question Image

at the centre of each edge (only one such void is shown)

8. Structure of Ionic Compounds:

Radius ratio $(\frac{r^{+}}{r})$ :

$\frac{r_{+}}{r_{-}}$	Geometry	Co-ordination number	Example
$0.155 < \frac{r_{+}}{r_{-}} < 0.225$	Triangular planar	$3$	$B_{2} O_{3}$
$0.225 < \frac{r_{+}}{r_{-}} < 0.414$	Tetrahedral	$4$	$Z n S$
$0.414 < \frac{r_{+}}{r_{-}} < 0.732$	Octahedral	$6$	$N a C l$
$0.732 < \frac{r_{+}}{r_{-}} < 1$	Cubic	$8$	$C s C l$

(i) Rock salt $(N a C l)$ type structure:

Characteristics:

(a) It has $f c c$ or $c c p$ arrangement in which $C l^{-}$ ions occupy the corners and face centres of a cube while $N a^{+}$ occupy body centres and edge centres (Octahedral voids).

(b) This structure has a $6 : 6$ coordination number.

(c) A unit cell of $N a C l$ consists of $4 N a^{+}$ ion and $4 C l^{-}$ ions.

Examples: Alkali metal halides (except $C s$ ), Halides of $A g$ (except $A g I$ ).

(ii) Caesium chloride $(C s C l)$ type structure:

Characteristics:

(a) It has $b c c$ arrangement.

(b) This structure has $8 : 8$ coordination number.

(c) The unit cell of $C s C l$ consists of one ${C s}^{+}$ ion at body centre and eight $C l^{-}$ ion at each corner i.e., one $C s C l$ formula unit per unit cell.

Example: $C s B r, C s l, C s C N, T l C l, T l B r, T l I, T l C N .$

(iii) Zinc blende or Sphalerite $(Z n S)$ type structure:

Characteristics:

(a) It has a $c c p$ arrangement in which $S^{2 -}$ ions are present at the corners as well as at the centre of each face of the cube.

(b) ${Z n}^{+ 2}$ ions are present at alternate tetrahedral void [ $50 %$ of tetrahedral void.]

(c) This structure has a $4 : 4$ coordination number.

Example: $C u C l, C u B r, C u I, A g I$ , and $B e S .$

Other important structures are-

(iv) Fluorite $(C a F_{2})$ type structure:

Characteristics:

(a) It has $c c p$ arrangement in which $C a^{2 +}$ ions are present at the corners as well as at the centre of each face of the cube.

(b) $F^{-}$ ions are present in all tetrahedral voids.

(c) This structure has a $8 (c a t i o n) : 4 (a n i o n)$ coordination number.

Examples: ${M g F}_{2}, {Z r O}_{2}, {S r F}_{2}$

(v) Anti-Fluorite $({N a}_{2} O)$ type structure:

Characteristics:

(a) It has a $c c p$ arrangement in which $O^{2 -}$ ions are present at the corners as well as at the centre of each face of the cube.

(b) ${N a}^{+}$ ions are present in all tetrahedral voids.

(c) This structure has a $4 (c a t i o n) : 8 (a n i o n)$ coordination number.

Examples: $K_{2} O, L i O, {N a}_{2} O$ and $K_{2} S$ .

(vi) Wurtzite $(Z n S)$ type structure:

Characteristics:

(a) It has a $h c p$ arrangement in which ${Z n}^{2 +}$ ions are present at each lattice point of $hcp$ .

(b) $S^{2 -}$ ions are present at $50 %$ of the tetrahedral voids (alternate).

(c) This structure has a $4 : 4$ coordination number.

(d) A unit cell consists of $6 Z n^{2 +}$ ions and $6 S^{2 -}$ ions.

Example: $C u C l, C u B r, C u I, A g I$ , and $B e S$ (Same as zinc blende).

9. Imperfection in Solids:

Schottky defect

Frenkel defect

F

-centre

Equal number of cations and anions are missing from their respective position leaving behind a pair of holes.

This type of defect is created when an ion leaves its appropriate site in the lattice and occupies an interstitial site.

A compound may have excess metal ions if an anion (negative ion) is absent from its appropriate lattice site creating a 'void' which is occupied by an electron.

Density decrease.

Coordination number is high.

Limiting radius ratio is high

Electrically neutral

Ex. $N a C l, C s C l, K C l, K B r$ etc.

Density unchanged

Coordination number is low.

Limiting radius ratio is low

Electrically neutral Ex. $Z n S, A g B r, A g C l$ etc.

Ex. $N a C l \to$ Yellow

$K C l \to$ Violet

Note: $A g B r$ shows both Schottky and Frenkel defects.

10. Electrical and Magnetic Properties of Solids:

(i) Electrical Properties:

Solids can be classified into three types based on their conductivities.

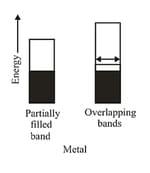
(a) Conductors: The solids with conductivities ranging between $10^{4}$ to $10^{7} {o h m}^{- 1} m^{- 1}$ are called conductors. Metals have conductivities in the order of $10^{7} {o h m}^{- 1} m^{- 1}$ are good conductors. The atomic orbitals of metal atoms form molecular orbitals which are so close in energy to each other as to form a band. If this band is partially filled or it overlaps with a higher energy unoccupied conduction band, the electrons can flow easily under an applied electric field and the metal shows conductivity.

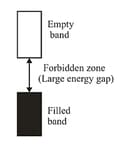
Question Image

(b) Insulators: These are the solids with very low conductivities ranging between $10$ ^–20 to $10$ ^–10 ${o h m}^{- 1} m^{- 1}$ . If the gap between filled-valence band and the next higher-unoccupied band (conduction band) is large, electrons cannot jump to it and such a substance has very small conductivity and it behaves as an insulator.

Question Image

(c) Semiconductors: These are the solids with conductivities in the intermediate range from $10^{- 6}$ to $10^{4} {o h m}^{- 1} m^{- 1}$ . In case of semiconductors, the gap between the valence band and conduction band is small. Therefore, some electrons may jump to the conduction band and show some conductivity.

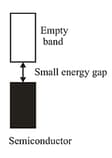
Question Image

Electrical conductivity of semiconductors increases with rise in temperature, since more electrons can jump to the conduction band. Substances like silicon and germanium show this type of behaviour and are called intrinsic semiconductors.

Their conductivity is increased by adding an appropriate amount of suitable impurity. This process is called doping.

(ii) Electron-rich impurities:

Silicon and germanium, when doped with a group $15$ element like $P$ or $A s$ , which contains five valence electrons, they occupy some of the lattice sites in silicon or germanium crystal.

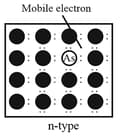
Question Image

Four out of five electrons are used in the formation of four covalent bonds with the four neighbouring silicon atoms. The fifth electron is extra and becomes delocalised. These delocalised electrons increase the conductivity of doped silicon (or germanium). Here the increase in conductivity is due to the negatively charged electron; hence, silicon doped with electron-rich impurity is called $n$ -type semiconductor.

(iii) Electron – deficient impurities:

Silicon or germanium when doped with a group $13$ element like $B, A l$ or $G a$ which contains only three valence electrons. The place where the fourth valence electron is missing is called electron hole or electron vacancy.

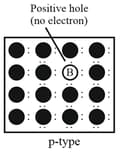
Question Image

Under the influence of electric field, electrons would move towards the positively charged plate through electronic holes, but it would appear as if electron holes are positively charged and are moving towards negatively charged plate. This type of semiconductors are called $p$ -type semiconductors.

(iv) Magnetic Properties:

On the basis of their magnetic properties, substances can be classified into five categories:

(v) Paramagnetic:

(a) Magnetised in a magnetic field in the same direction.

(b) Lose their magnetism in the absence of magnetic fields.

(c) Presence of one or more unpaired electrons which are attracted by the magnetic field.

(d) Examples – $O_{2}, {C u}^{2 +}, {F e}^{3 +}, {C r}^{3 +}$

(vi) Diamagnetism:

(a) Weakly magnetised in a magnetic field in the opposite direction.

(b) All the electrons are paired and there are no unpaired electrons.

(vii) Ferromagnetism:

(a) Very strongly attracted by a magnetic field.

(b) Examples – iron, cobalt, nickel, gadolinium and ${C r O}_{2}$ .

(c) In solid state, the metal ions of ferromagnetic substances are grouped together into small regions called domains. Thus, each domain acts as a tiny magnet.

(d) In the absence of magnetic fields, the domains are randomly oriented, and their magnetic moments get cancelled.

(e) In a magnetic field, all the domains get oriented in the direction of the magnetic field and a strong magnetic effect is produced.

Question Image