Relative to the origin , the position vectors of points and are given by
It is given that . Find the angle

Important Questions on Vectors
Find the vector equation of the line .
Find whether or not the vectors and are perpendicular.
With respect to the origin , the position vectors of the points and are given by
Write down the vector
With respect to the origin O, the position vectors of the points A and B are given by
Find a vector equation of the line .
The vector equation of the line is given by
Show that the lines and intersect and find the position vector of the point of intersection.
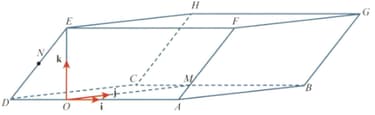
The diagram shows a prism, , with a parallelogram-shaped uniform cross-section.
The point is such that is the height of the parallelogram. The point is such that is parallel to and N is the midpoint of . The side OD has a length of units. The unit vectors and are parallel to and , respectively.
The position vectors of the points and are given by and
Express the vectors and in terms of and
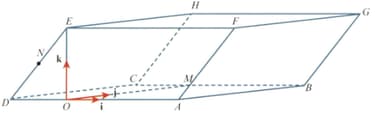
The diagram shows a prism, , with a parallelogram-shaped uniform cross-section.
The point is such that is the height of the parallelogram. The point is such that is parallel to and is the midpoint of . The side OD has a length of units. The unit vectors and are parallel to and , respectively.
The position vectors of the points and are given by and
Use a vector method to find angle
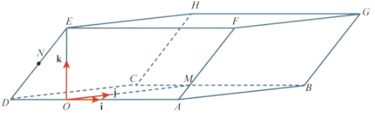
The diagram shows a prism, , with a parallelogram-shaped uniform cross-section.
The point is such that is the height of the parallelogram. The point M is such that is parallel to and N is the midpoint of . The side OD has a length of units. The unit vectors and are parallel to and , respectively.
The position vectors of the points and are given by and
Write down a vector equation of the line
