MEDIUM
Earn 100
Show that the diagonal of a rectangle divides it in two congruent triangles.
Important Questions on Congruence of Triangles
HARD
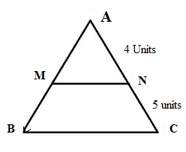
MEDIUM
MEDIUM
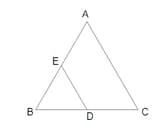
EASY
In the given figure, if and , then the measure of is:
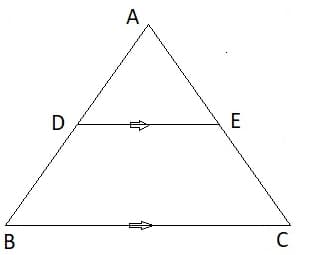
HARD
MEDIUM
MEDIUM
MEDIUM
HARD
Let be a triangle and be a point on side closer to vertex than . Let be a point on side such that is parallel to and let be a point on side such that is parallel to . If the area of the quadrilateral is equal to of the area of , then the ratio equals
MEDIUM
EASY
HARD
In a triangle with points are on the interior of segments respectively. Which of the following triangles cannot be similar to the triangle ?
MEDIUM
MEDIUM
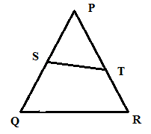
EASY
HARD
EASY
MEDIUM
HARD
HARD
