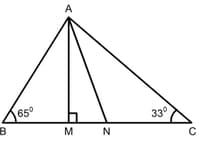
EASY
Earn 100
State the converse of angle bisector theorem.
Important Questions on Triangles
MEDIUM
MEDIUM
MEDIUM
MEDIUM
HARD
MEDIUM
EASY
HARD
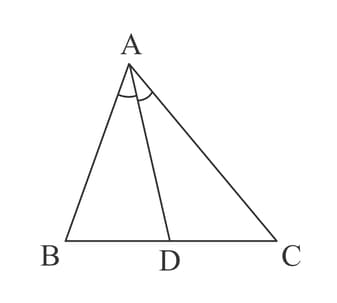
In , it is given that Find in degrees.
MEDIUM
EASY
EASY
MEDIUM
EASY
In the given figure, is the bisector of . If and . Find .
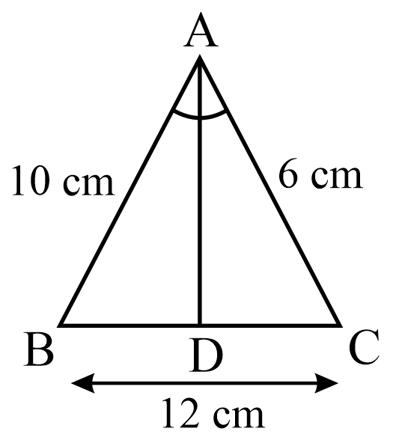
EASY
In , the bisector of intersects in . If then _____.
MEDIUM
In the given fig. and is the bisector of . If and , then the value of will be
MEDIUM
EASY
Let be the side-length of a triangle and be the lengths of its medians. Put Then, as vary, can assume every value in the interval
MEDIUM
HARD
MEDIUM
If all the vertices of an isosceles right angle triangle be integral points and length of base is also an integer, then which of the point is never a rational point (A point is integral point if both `x` and `y` are integers and point is rational, if both `x` and `y` are rational).