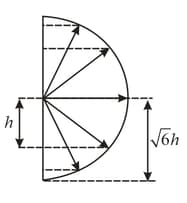
The angular momentum of electrons in an atom and this spatial orientations can be depicted schematically by a vector diagram where the length of the vector is proportional to the absolute value of the orbital angular momentum of an electron. What vectors in the diagram correspond to the minimal value of the principal quantum number $n$ and what are the values of the quantum numbers $l$ and $m ?$ 

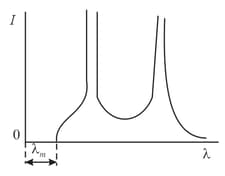
The intensity distribution of $X$-ray radiation over wavelengths consists of a continuous spectrum, which is limited from the short-wave side by a limit wavelength ${\lambda }_m$, and a characteristic spectrum, which consists of separate peaks. In the figure (with an arbitrary scale) we depict such a distribution for a voltage $U_1$ applied to the $X$-ray tube. How will the distribution change if the voltage is decreased three-fold, that is, $U_2=\left(\frac{1}{3}\right)U_1 ?$ 

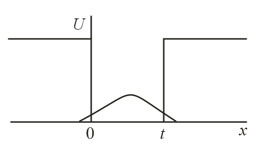
An electron is inside a potential well with vertical walls. The electronic wave function is depicted in the figure. Is the depth of the well finite or infinite?

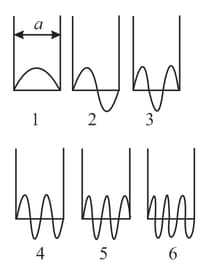
An electron is in motion in a potential well of infinite depth. Depending on the electron kinetic energy, the electronic wave function has different configurations depicted in the figure. Which of these states is retained when the width of the potential well is decreased two-fold? By what factor will the minimal kinetic energy of the electron change in the process?

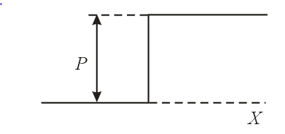
From the viewpoint of the optical analogy of the wave properties of an electron, the regions of space where it possesses different potential energies may be interpreted as regions with different refractive indices. In the figure two such regions are depicted, the regions are separated by a boundary where the potential energy$P$ experiences a jump. In which of these regions is the refractive index greater? In which of the two cases, when the electron moves from left to right or when it moves from right to left, will the phase of the wave function be retained under reflection of the electron from the barrier, and in which will it change to its opposite?

An electron moving from left to right meets an obstacle, which in one case is a step (Figure (a)), and in the other a barrier (Figure (b)). What are the probabilities of the electron overcoming the step and the barrier according to the classical theory and the quantum theory in two separate cases, namely, when the electron kinetic energy $E$ is lower than $P$ and when it is higher than $P ?$ 

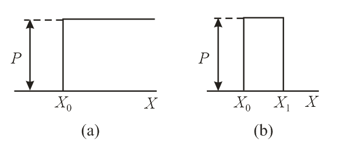
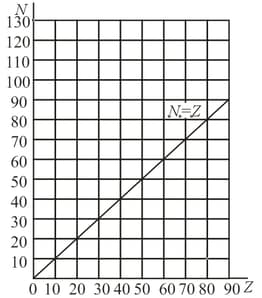
The number of protons and the number of neutrons in the nuclei of stable isotopes are laid off on the horizontal and vertical axes, respectively. Why does the fraction of neutrons in the overall number of nucleons increase with the mass number of the nuclei?