The curve $y = a x^{2} + b x + c$ passes through the point $(1, 2)$ and its tangent at origin is the line $y = x .$ The area bounded by the curve, the abscissa of the curve at minima and the tangent line is:

50% studentsanswered this correctly

Important Points to Remember in Chapter -1 - Area of Bounded Regions from Amit M Agarwal Skills in Mathematics for JEE MAIN & ADVANCED INTEGRAL CALCULUS Solutions

1. Area Under the Curve:

(i) Area bounded by the curve $y = f (x)$ , $x$ -axis and the ordinates $x = a$ and $x = b$ is given by

$A = \int_{a}^{b} |f (x)| d x = \int_{a}^{b} |y| d x$ .

(Note: Here, modulus is used because of the convention to consider the magnitude of area only, whether $f (x)$ is below or above the $x$ -axis.)

(ii) Area bounded by the curve $x = f (y)$ , $y$ -axis and abscissa $y = c, y = d$ is given by

$A = \int_{c}^{d} |x| d y = \int_{c}^{d} |f (y)| d y$ .

2. Area Bounded by Curves:

Area bounded between the curves $f (x)$ and $g (x)$ from $x = a$ to $x = b$ is given by

$A = \int_{a}^{b} |f (x) - g (x)| d x$ , Now use the property $\int_{a}^{b} |f (x)| d x = \int_{a}^{c} f (x) d x + \int_{c}^{b} f (x) d x$ , wherever it is required to define the modulus.

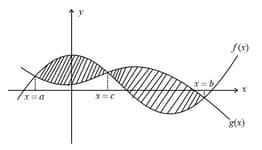
Question Image

For example-Shaded area in the above diagram is $A = \int_{a}^{b} |f (x) - g (x)| d x = \int_{a}^{c} \{f (x) - g (x)\} d x + \int_{c}^{b} \{g (x) - f (x)\} d x$

3. Curve Tracing:

To find approximate shape of a curve, the following phrases are suggested:

(i) Symmetry:

(a) Symmetry about $x$ -axis:

If all the powers of ' $y$ ' in the equation are even then the curve (graph) is symmetrical about the $x$ -axis.

E.g.: $y^{2} = 4 a x$

(b) Symmetry about $y$ -axis:

If all the powers of ' $x$ ' in the equation are even then the curve (graph) is symmetrical about the ' $y$ ' -axis.

E.g.: $x^{2} = 4 a y$

(c) Symmetry about both axis:

If all the powers of ' $x$ ' and ' $y$ ' in the equation are even then the curve (graph) is symmetrical about the ' $x$ ' as well as ' $y$ ' -axis.

E.g.: $x^{2} + y^{2} = a^{2}$

(d) Symmetry about the line $y = x$

If the equation of the curve remain unchanged on interchanging ' $x$ ' and ' $y$ ' then the curve (graph) is symmetrical about the line $y = x .$

E.g.: $x^{3} + y^{3} = 3 a x y$

(e) Symmetry in opposite quadrants:

If the equation of the curve (graph) remain unaltered when ' $x$ ' and ' $y$ ' are replaced by $- x$ and $- y$ respectively, then there is symmetry in opposite quadrants.

(ii) Find the points where the curve crosses the $x$ -axis and the $y$ -axis.

(iii) Find $\frac{d y}{d x}$ and equate it to zero to find the points on the curve where you have horizontal tangents.

(iv) Examine intervals when $f (x)$ is increasing or decreasing.

(v) Examine what happens to ' $y$ ' when $x \to \infty$ or $x \to - \infty$