The diagram shows a triangular prism, $OABCDE.$ The uniform cross-section of the prism, $OAE,$ is a right-angled triangle with base $77 \mathrm{cm}$ and height $36 \mathrm{cm}.$ The length, $AB,$ of the prism is $60 \mathrm{cm}.$ The unit vectors $i, j$ and $k$ are parallel to $\overrightarrow{OA},\overrightarrow{OC}$ and $\overrightarrow{OE},$ respectively. The point $N$ divides the length of the line $DB$ in the ratio $4 : 1$ and $M$ is the midpoint of $DE.$

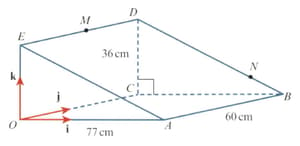
Use a scalar product to find angle $MAN.$

The diagram shows a pyramid $VOABC.$ The base of the pyramid, $OABC,$ is a rectangle. The unit vectors $i, j$ and $k$ are parallel to $\overrightarrow{OA},\overrightarrow{OC}$ and $\overrightarrow{OV},$ respectively. The position vectors of the points$A, B, C$ and $V$ are given by
$\overrightarrow{OA}=6i,\overrightarrow{ OC}=3j \mathrm{and} \overrightarrow{O\overrightarrow{V}}=9k.$
The points $M$ and $N$ are the midpoints of$AB$ and $BV,$ respectively.

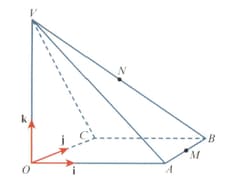
Find the angle between the directions of $\overrightarrow{AN}$ and $\overrightarrow{OC}.$

The diagram shows a pyramid $VOABC.$ The base of the pyramid, $OABC,$ is a rectangle. The unit vectors $i, j$ and $k$ are parallel to $\overrightarrow{OA},\overrightarrow{OC}$ and $\overrightarrow{OV},$ respectively. The position vectors of the points$A, B, C$ and $V$ are given by
$\overrightarrow{OA}=6i,\overrightarrow{ OC}=3j \mathrm{and} \overrightarrow{O\overrightarrow{V}}=9k.$
The points $M$ and $N$ are the midpoints of$AB$ and $BV,$ respectively.

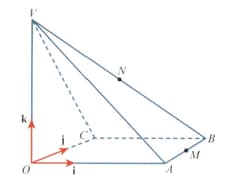
Find the vector $\overrightarrow{MN}.$

The diagram shows a pyramid $VOABC.$ The base of the pyramid, $OABC,$ is a rectangle. The unit vectors $i, j$ and $k$ are parallel to $\overrightarrow{OA},\overrightarrow{OC}$ and $\overrightarrow{OV},$ respectively. The position vectors of the points$A, B, C$ and $V$ are given by
$\overrightarrow{OA}=6i,\overrightarrow{ OC}=3j \mathrm{and} \overrightarrow{O\overrightarrow{V}}=9k.$
The points $M$ and $N$ are the midpoints of$AB$ and $BV,$ respectively.

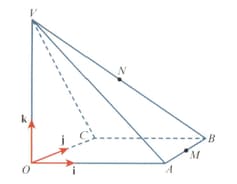
The point $P$ lies on $OV$ and is such that $PNM$ is a right angle. Find the position vector of the point $P.$

Write down the vector equation for the line through the point$A$ that is parallel to vector $b$ when:

$A\left(0, -1, 5\right)$ and $b=2i+6j-k$

Write down the vector equation| for the line through the point$A$ that is parallel to vector $b$ when:

$A\left(0, 0, 0\right)$ and $b=7i-j-k$

Write down the vector equation| for the line through the point$A$ that is parallel to vector $b$ when:

$A\left(7, 2, -3\right)$ and $b=3i-4k$

The vector equation for the lines are:

$r=-j+5k+\lambda \left(2i+6j-k\right)$

$r=\lambda \left(7i-j-k\right)$

$r=7i+2j-3k+\lambda \left(3i-4k\right)$

Write equation of lines in parametric form.