In the figure, A B C D E F is a regular hexagon and P Q R is an equilateral triangle of side ' a '. The area of the shaded portion is 23 3 c m 2 and C D : P Q : : 2 : 1 . If the area of the circle circumscribing the hexagon is X π c m 2 then X = ?

According to the question, area of Hexagon = Area of six equilateral triangles having their side equal to the side of the hexagon = 6 × √ 3 / 4 × ( 2 a ) 2 = 6 √ 3 a 2 . Area of PQR = ( √ 3 / 4 ) × a ² = = √ 3 / 4 a ² . Difference = √ 3 a ² ( 6 - 1 / 4 ) = ³ = ( 23 / 4 ) ( √ 3 a ² ) . A ² = 4 × 23 √ 3 / 23 √ 3 ⇒ a ² = 4 . Now, we know for such circles circumscribed around a regular hexagon, the radius of the circle is equal to the side of the hexagon. Hence, the radius of theCircle is 2 a . Area of circle = πr ² = π ( 2 a ) ² = 4 πa ² = 4 π × 4 = 16 π cm ² Therefore a ² = 4 . Hence, the correct answer is x = 16 .

EASY

CAT

IMPORTANT

Earn 100

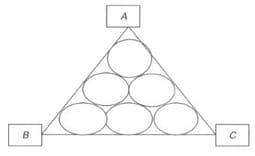
The diagram shows six equal circles inscribed in equilateral triangle $A B C$ . The circles touch externally among themselves and also touch the sides of the triangle. If the radius of each circle is $R$ , area of the triangle is

50% studentsanswered this correctly

Important Questions on Geometry and Mensuration

EASY

CAT

IMPORTANT

How to prepare for Quantitative Aptitude for the CAT>Chapter 16 - Geometry and Mensuration>Level of Difficulty>Q 46

A boy Mithilesh was playing with a square cardboard of side $2$ meters. While playing, he accidentally sliced off the corners of the cardboard in such a manner that a figure having all its sides equal was generated. The area of this eight-sided figure is:

EASY

CAT

IMPORTANT

How to prepare for Quantitative Aptitude for the CAT>Chapter 16 - Geometry and Mensuration>Level of Difficulty>Q 47

In a painting competition, students were asked to draw alternate squares and circle, circumcribing each other. The first student drew

A_{1}

a square whose side is 'a' meters. The second student drew Circle

C_{1}

circumscribing the square

A_{1}

such that all its vertices are on

C_{1}

. Subsequent students, drew square

A_{2}

circumscribing

C_{1}

, Circle

C_{2}

circumscribing

A_{2}

and

A_{3}

circumscribing

C_{2}

, and so on. If

D_{N}

is the area between the square AN and the circle

C_{N}

, where

N

is a natural number, then the ratio of the sum of all

D_{N}

D_{1}

for

N = 12

is:

EASY

CAT

IMPORTANT

How to prepare for Quantitative Aptitude for the CAT>Chapter 16 - Geometry and Mensuration>Level of Difficulty>Q 49

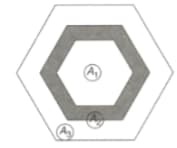
In the figure, $A B C D E F$ is a regular hexagon and $P Q R$ is an equilateral triangle of side ' $a$ '. The area of the shaded portion is $23 \sqrt{3} c m^{2}$ and $C D : P Q : : 2 : 1$ .

If the area of the circle circumscribing the hexagon is $X π c m^{2}$ then $X = ?$

Question Image

EASY

CAT

IMPORTANT

How to prepare for Quantitative Aptitude for the CAT>Chapter 16 - Geometry and Mensuration>Level of Difficulty>Q 51

At the centre of a city's municipal park there is a large circular pool. A fish is released in the water at the edge of the pool. The fish swims north for

30

meters before it hits the edge of the pool. It then turns east and swims for

40

meters before it hits the edge of the pool. If the area of the pool is

X π m^{2}

the

X =

EASY

CAT

IMPORTANT

How to prepare for Quantitative Aptitude for the CAT>Chapter 16 - Geometry and Mensuration>Level of Difficulty>Q 54

A circular road is constructed outside a square field. The perimeter of the square field is

200

ft. If the width of the road is

7 \sqrt{2}

ft and cost of construction is

₹ 100

per sq. ft. Find the lowest possible cost to construct

50 %

of the total road.

EASY

CAT

IMPORTANT

How to prepare for Quantitative Aptitude for the CAT>Chapter 16 - Geometry and Mensuration>Level of Difficulty>Q 56

Consider a rectangle

A B C D

of area

90

units. The points

P

and

Q

trisect

A B

, and

R

bisects

C D

. The diagonal

A C

intersects the line segments

P R

and

Q R

M

and

N

respectively. What is the area of the quadrilateral

P Q N M

EASY

CAT

IMPORTANT

How to prepare for Quantitative Aptitude for the CAT>Chapter 16 - Geometry and Mensuration>Level of Difficulty>Q 63

Three regular hexagons are drawn such that their diagonals cut each other at the same point and area $A_{1} : A_{2} : A_{3} = 1 : 2 : 3$ . Then the ratio of the length of the sides of the regular hexagons (from the smallest to the largest) is:

Question Image

EASY

CAT

IMPORTANT

How to prepare for Quantitative Aptitude for the CAT>Chapter 16 - Geometry and Mensuration>Extra Practice Exercise on Geometry and Mensuration>Q 1

In the figure given what is the measure of

∠ A C D

The diagram shows six equal circles inscribed in equilateral triangle ABC. The circles touch externally among themselves and also touch the sides of the triangle. If the radius of each circle is R, area of the triangle is

Important Questions on Geometry and Mensuration

Learn and Prepare for any exam you want !

The diagram shows six equal circles inscribed in equilateral triangle $A B C$ . The circles touch externally among themselves and also touch the sides of the triangle. If the radius of each circle is $R$ , area of the triangle is