A thin horizontal uniform rod A B , of mass m , and length l , can rotate freely about a vertical axis passing through its end A . At a certain moment, the end B , starts experiencing a constant force F → , which is always perpendicular to the original position of the stationary rod and directed in a horizontal plane. Find the angular velocity of the rod as a function of its rotation angle φ , counted relative to the initial position.

Let us assume that, the rod of length l , has rotated an angle φ , from its initial position in time t . Now, resolve the force F , along the length and perpendicular to the length of the rod. Component of force along the length= F sin φ Component of force perpendicular to rod= F cos φ At that instant, for the rotating rod, Torque = N z = F sin φ × 0 + F cos φ × l = F cos φ × l (only perpendicular component will be responsible for torque) Hence, by work kinetic energy theorem, the gain in rotational kinetic energy Δ T is equal to the work done by the torque. Δ T = W ext Hence, 1 2 I ω 2 = ∫ N z d φ (initially rod was at rest) ⇒ 1 2 I ω 2 = ∫ 0 ϕ F cos φ d ϕ = F sin ϕ ⇒ ω = 6 F sin φ M l

HARD

JEE Main

IMPORTANT

Earn 100

The ends of thin threads, tightly wound on the axle of radius $r$ , of the Maxwell disc, are attached to a horizontal bar. When the disc unwinds, the bar is raised to keep the disc at the same height. The mass of the disc with the axle is equal to $m$ , and the moment of inertia of the arrangement, relative to its axis, is $I$ . Find the tension of each thread and the acceleration of the bar.

Important Questions on PHYSICAL FUNDAMENTALS OF MECHANICS

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 1 - PHYSICAL FUNDAMENTALS OF MECHANICS>DYNAMIC OF A SOLID BODY>Q 1.245.

A thin horizontal uniform rod $A B$ , of mass $m$ , and length $l$ , can rotate freely about a vertical axis passing through its end $A$ . At a certain moment, the end $B$ , starts experiencing a constant force $\vec{F}$ , which is always perpendicular to the original position of the stationary rod and directed in a horizontal plane. Find the angular velocity of the rod as a function of its rotation angle $φ$ , counted relative to the initial position.

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 1 - PHYSICAL FUNDAMENTALS OF MECHANICS>DYNAMIC OF A SOLID BODY>Q 1.246.

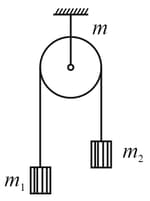
In the arrangement shown in the figure, the mass of the uniform solid cylinder, of radius $R$ , is equal to $m$ , and the masses of two bodies are equal to $m_{1}$ and $m_{2}$ . The thread slipping and the friction in the axle of the cylinder are supposed to be absent. Find the angular acceleration of the cylinder and the ratio of tensions, $\frac{T_{1}}{T_{2}}$ , of the vertical sections of the thread in the process of motion.

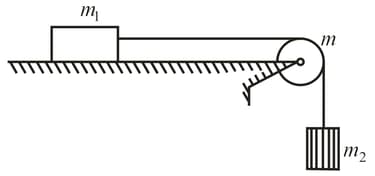
Question Image

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 1 - PHYSICAL FUNDAMENTALS OF MECHANICS>DYNAMIC OF A SOLID BODY>Q 1.247.

In the system shown in the figure, the masses of the bodies are known to be $m_{1}$ and $m_{2}$ , the coefficient of friction between the body $m_{1}$ and the horizontal plane is equal to $k$ , and a pulley of mass $m$ , is assumed to be a uniform disc. The thread does not slip over the pulley. At the moment $t = 0$ , the body $m_{2}$ , starts descending. Assuming the mass of the thread and the friction in the axle of the pulley to be negligible, find the work performed by the friction forces acting on the body $m_{1}$ , over the first $t$ seconds, after the beginning of the motion.

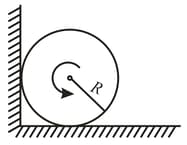
Question Image

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 1 - PHYSICAL FUNDAMENTALS OF MECHANICS>DYNAMIC OF A SOLID BODY>Q 1.248.

A uniform cylinder of radius $R$ is spinned about its axis to the angular velocity $ω_{0}$ and then placed in a corner. The coefficient of friction between the corner walls and the cylinder is equal to $k$ . How many turns will the cylinder accomplish before it stops?

Question Image

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 1 - PHYSICAL FUNDAMENTALS OF MECHANICS>DYNAMIC OF A SOLID BODY>Q 1.249.

A uniform disc of radius

R

is spinned to the angular velocity

ω

and then carefully placed on a horizontal surface. How long will the disc be rotating on the surface, if the friction coefficient is equal to

k

? The pressure exerted by the disc on the surface can be regarded as uniform.

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 1 - PHYSICAL FUNDAMENTALS OF MECHANICS>DYNAMIC OF A SOLID BODY>Q 1.250.

A flywheel, with the initial angular velocity

ω_{0}

, decelerates due to the forces whose moment, relative to the axis, is proportional to the square root of its angular velocity. Find the mean angular velocity of the flywheel averaged over the total deceleration time.

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 1 - PHYSICAL FUNDAMENTALS OF MECHANICS>DYNAMIC OF A SOLID BODY>Q 1.251.

A uniform cylinder, of radius $R$ and mass $M$ , can rotate freely about a stationary horizontal axis $O$ . A thin cord, of length $l$ and mass $m$ , is wound on the cylinder in a single layer. Find the angular acceleration of the cylinder as a function of the length $x$ of the hanging part of the cord. The wound part of the cord is supposed to have its centre of gravity on the cylinder axis.

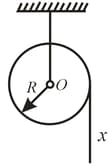
Question Image

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 1 - PHYSICAL FUNDAMENTALS OF MECHANICS>DYNAMIC OF A SOLID BODY>Q 1.253.

A uniform cylinder of mass $m = 8.0 kg$ , and radius $R = 1.3 cm$ , starts descending, at a moment $t = 0$ , due to gravity. Neglecting the mass of the thread, find:

$(a)$ the tension of each thread and the angular acceleration of the cylinder;
$(b)$ the time dependence of the instantaneous power developed by the gravitational force.

Question Image

$(Gravitational acceleration g = 9.8 m s^{- 2})$

Important Questions on PHYSICAL FUNDAMENTALS OF MECHANICS

Learn and Prepare for any exam you want !