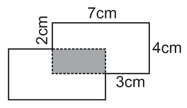
The figure is made up of two identical rectangles. Find the area of the shaded part:

(i) A square centimetre is the area of the region formed by a square of side $1 \mathrm{cm}$.

(ii) Standard units of area and their relations are:

(a) $100\mathrm{ }{\mathrm{mm}}^2=1\mathrm{ }{\mathrm{cm}}^2,100\mathrm{ }{\mathrm{cm}}^2=1\mathrm{ }{\mathrm{dm}}^2$
(b) $100\mathrm{ }{\mathrm{dm}}^2=1\mathrm{ }{\mathrm{m}}^2,10000\mathrm{ }{\mathrm{cm}}^2=1\mathrm{ }{\mathrm{m}}^2$
(c) $100\mathrm{ }{\mathrm{m}}^2=1 \mathrm{are},100\mathrm{ }\mathrm{ares}=1 \mathrm{hectare}$
(d) $10 \mathrm{hectares}=1\mathrm{ }\mathrm{sq}.\mathrm{km}$

2. Perimeter and Area of a Rectangle and a Square:

(i) Perimeter of a rectangle $=2\left(\mathrm{Length}+\mathrm{Breadth}\right)$ or $P=2\left(l+b\right)$.

(ii) Perimeter of a square $=4\left(\mathrm{Side}\right) \mathrm{or} P=4I$.

(iii) Area of a rectangle $= \text{Length}\times \text{Breadth} \text{or} A=I\times b$.

(iv) Length of a rectangle $=\frac{\mathrm{Area}}{\mathrm{Breadth}} \text{or} l=\frac{A}{b}$.

(v) Breadth of a rectangle $=\frac{\mathrm{Area}}{\mathrm{Length}} \text{or} b=\frac{A}{l}$.

(vi) Area of a square $={\left(\mathrm{Side}\right)}^2 \mathrm{or} A=l\times l$.

3. Parallelogram:

(i) Area of a parallelogram $=\text{Base}\times \text{Height} \text{or} A=b\times h$.

(ii) Base of parallelogram $=\frac{\mathrm{Area}}{\mathrm{height}} \text{or} b=\frac{A}{h}$.

(iii) Height of a parallelogram $=\frac{\mathrm{Area}}{\mathrm{base}} \text{or} h=\frac{A}{b}$.

4. Triangle:

(i) Area of a triangle $=\frac{1}{2}\times \text{Base}\times \text{Height} \text{or} A=\frac{1}{2}\times b\times h$.

(ii) Height of a triangle $=\frac{2\times \mathrm{Area}}{\mathrm{Base}} \text{or} h=\frac{2A}{b}$.

(iii) Base of a triangle $=\frac{2\times \mathrm{Area}}{\mathrm{height}} \text{or} b=\frac{2A}{h}$.

5. Rhombus:

Area of a rhombus $=\frac{1}{2}\times$ (Product of diagonals)

6. Trapezium:

Area of trapezium $=\frac{1}{2}\times$ (Sum of the parallel sides) $\times$ (perpendicular distance between the parallel sides)

7. Perimeter and Area of Circle:

(i) The perimeter of a circle is called its circumference.

(ii) The ratio of the circumference of a circle to its diameter is the same for all circles, regardless of their sizes. The constant ratio is denoted by π whose approximate value is 227 or $3.14$.$\begin{array}{l}i.e.\frac{\mathrm{Circunference}}{\mathrm{Diameter}}=\mathrm{\pi }\end{array}$

$\Rightarrow \frac{C}{2r}=\mathrm{\pi }$, where $C$ is the circumference of the circle and $r$ is the radius of the circle

$\Rightarrow C=2\mathrm{\pi }r$.

(iii) The number π is not a rational number.

(iv) Circumference $C$ of a circle of radius $r$ is given by $C=2\pi r$. Or, $C=\mathrm{\pi }d$, where $d=2r=$ Diameter.

(v) Area $A$ of a circle of radius $r$ is given by $A=\pi r^2$.

(vi) Radius of a circle $=\sqrt{\frac{A}{\pi }}$.