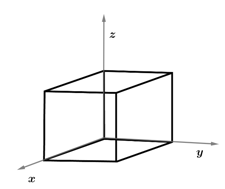
The figure shows a cube of side $l$ with edges parallel to the axes. The electric field is in positive $y$ direction but its magnitude changes such that it is $\frac{15}{{\epsilon }_0{l}^2}$ at the bottom face and $\frac{5}{{\epsilon }_0{l}^2}$ at the top face in SI units. Find the charge enclosed by the cube.

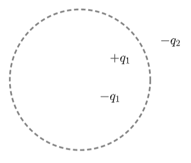
Consider the charge configuration and spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface, the electric field is due to

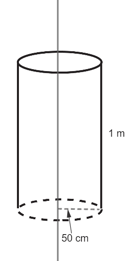
Electric charge is uniformly distributed along a long straight wire of radius $1 \mathrm{mm}$. The charge per cm length of the wire is $Q \mathrm{C} {\mathrm{cm}}^{-1}$ Coulomb. Another cylindrical surface of radius $50 \mathrm{cm}$ and length $1 \mathrm{m}$ symmetrically encloses the wire as shown in the figure. The total flux passing through the cylindrical surface is

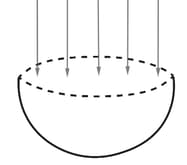
In the figure shown, a hemispherical bowl of radius $R$ is shown. Electric field of intensity $E$ is present perpendicular to the circular cross section of the hemisphere. The electric flux through the hemisphere is

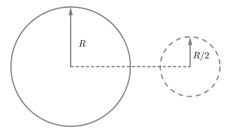
A ring of radius $R$ having a linear charge density $\lambda$ moves towards a solid imaginary sphere of radius $\frac{R}{2},$ so that the centre of ring passes through the centre of the sphere. The axis of the ring is perpendicular to the line joining the centres of the ring and the sphere. The maximum flux through the sphere in this process is

The electric field in a region is given by $\overrightarrow{E}=-4x\hat{\mathrm{i}}+6y\hat{\mathrm{j}}$. Then find the charge enclosed in the cube of side $1 \mathrm{m}$ oriented as shown in the diagram.