The force between two atoms in a diatomic molecule can be represented approximately by the potential energy function where and are constants.
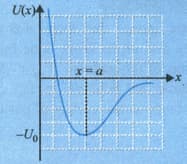
(a) At what value of is the potential energy zero?
(b) Find the force
(c) At what value of is the potential energy a minimum?

(b) Find the force
(c) At what value of is the potential energy a minimum?

Important Questions on Work, Energy and Power
A single conservative force acts on a particle that moves along -axis. The potential energy is given by, where is in meters. At the particle has kinetic energy
(a) What is the mechanical energy of the system.
(b) What are the least and greatest values of between which the particle can move.
(c) The maximum kinetic energy of the particle and value of at which it occurs.
(d) Determine the equation for as a function of
A conservative force has the potential energy function as shown in the graph. A particle moving in one dimensional under the influence of this force has kinetic energy when it is at position
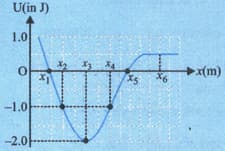
(a) Find the mechanical energy of the particle.
(b) Can the particle reach either or
(c) Find the least and greatest value of between which the particle can move.
A particle of mass is free to move along axis under influence of a conservative force. The potential energy function for the particle is given by
Where and If the total mechanical energy of the particle is zero,
(a) Plot this potential energy function, identify the regions where particle may be found
(b) Calculate the maximum speed of the particle.
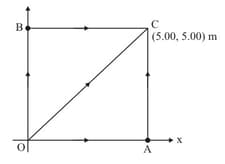
A particle moves in the plane in figure under the influence of a friction force with magnitude and acting in the direction opposite to the particle’s displacement. Calculate the work done by the friction force on particle as it moves along the following closed paths:
(a) path followed by the return path
(b) path followed by and the return path
(c) path followed by the return path
(d) each of your three answers should be non-zero.
What is the significance of this observation?