The given figure is an $x-t$ graph of the motion of a particle.

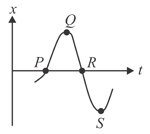
(i) At which of the points $P, Q, R$ and $S$, the velocity is $v_x$ positive?

(ii) At which points the velocity is negative?
(iii) At which points the velocity is zero?

(iv) At which of the points $P, Q, R$ and $S$ is the acceleration $a_x$ positive?

(v) At which point is the $a_x$ negative?
(vi) At which points does the acceleration appear to be zero?
(vii) At each point, state whether the speed is increasing, decreasing, or not changing.

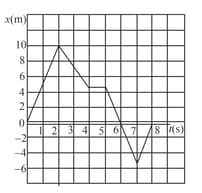
The position versus time graph for a certain particle moving along the $x$ -axis is shown in the figure. Find the average velocity in the time intervals

(a) $0$ to $2 \mathrm{s}$,

(b) $2 \mathrm{s}$ to $4 \mathrm{s}$, and

(c) $4 \mathrm{s}$ to $7 \mathrm{s}$.

The position-time $\left(x-t\right)$ graphs for two children $A$ and $B$ returning from their school $O$ to their homes $P$ and $Q$, respectively, are shown in figure. Choose the correct entries in the brackets below.

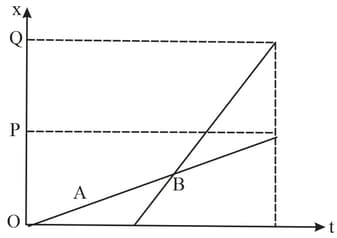
(a) $\left(\frac{A}{B}\right)$ lives closer to a school than $\left(\frac{B}{A}\right) .$

(b) $\left(\frac{A}{B}\right)$ starts from the school earlier than $\left(\frac{B}{A}\right)$.
(c) $\left(\frac{A}{B}\right)$ walks faster than $\left(\frac{B}{A}\right)$.
(d) $A$ and $B$ reach home at the (same/different) time.
(e) $\left(\frac{A}{B}\right)$ overtakes on the road (once/twice).

Describe the motion shown by the following velocity-time graphs.

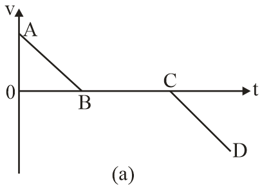
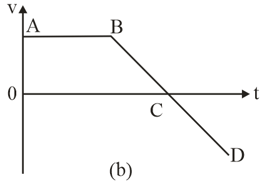
The velocity versus time curve of a moving point is shown in the figure. Find the retardation of the particle for the portion $CD$.

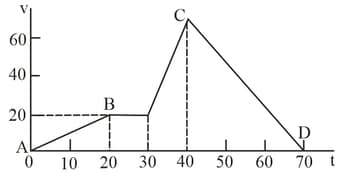
As soon as a car just starts from rest in a certain direction, a scooter moving with a uniform speed overtakes the car at that time. Their velocity-time graph is shown in the figure. Calculate

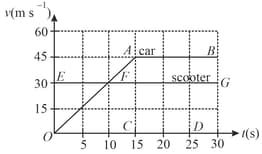
(a) The difference between the distances travelled by car and the scooter in $15 \mathrm{s}$.

(b) The distance of car and scooter from the starting point at that instant when the car catches scooter.

The velocity–time graph of a body moving along a straight line is given below. Find:

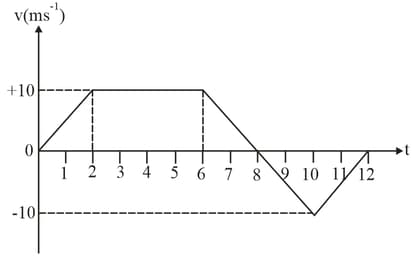
(a) Average velocity in whole time of motion
(b) Average speed in whole time of motion
(c) Draw acceleration vs time graph

A particle moves along $x$-axis with an initial speed $v_0=5{ \mathrm{m} \mathrm{s}}^{-1}$. If its acceleration varies with time as shown in $a-t$ graph in the figure,

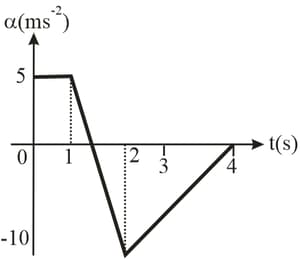
(a) Find| the velocity of the particle at $t=4 \mathrm{s}$.

(b) Find the time when the particle starts moving along $-x$-direction.

The given figure is a graph of the coordinate of a spider crawling along the $x$-axis.

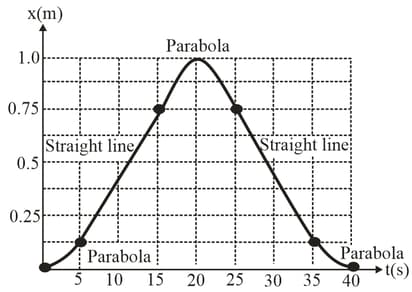
(a) Graph its velocity and acceleration as functions of time.

(b) In a motion diagram, show the position, velocity and acceleration of the spider at the five times: $t=2.5 \mathrm{s}, t=10 \mathrm{s}$, $t=20 \mathrm{s}, t=30 \mathrm{s}$ and $t=37.5 \mathrm{s}$.