MEDIUM
Earn 100
The graph between ratio of speed of electron in nth orbit to radius of nth orbit and n for Bohr’s hydrogen atom is
(a)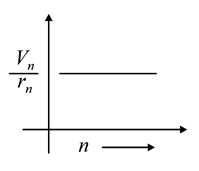

(b)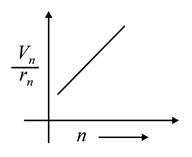

(c)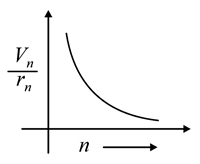

(d)None of these
69.34% studentsanswered this correctly
Important Questions on Atomic Physics
EASY
MEDIUM
Consider third orbit of (helium), using non-relativistic approach, the speed of electron in this orbit will be given constant , and (Planck's Constant)
EASY
MEDIUM
MEDIUM
MEDIUM
MEDIUM
MEDIUM
EASY
EASY
The magnitude of acceleration of the electron in the orbit of hydrogen atom is and that of singly ionised helium atom is . The ratio is,
MEDIUM
MEDIUM
MEDIUM
MEDIUM
HARD
MEDIUM
MEDIUM
MEDIUM
MEDIUM
MEDIUM

