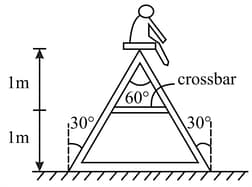
The ladder shown in figure has negligible mass and rests on a frictionless floor. The crossbar connects the two legs of the ladder at the middle. The angle between the two legs is ${60}^{\mathrm{o}}$. The fat person sitting on the ladder has a mass of $80\mathrm{}\mathrm{k}\mathrm{g}$. Find the contact forces exerted by the floor on each leg and the tension in the crossbar.

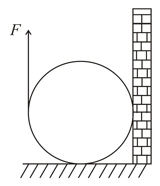
Figure shows a vertical force $F$ that is applied tangentially to a uniform cylinder of weight $W$. The coefficient of static friction between the cylinder and all surfaces is $0.5$. Find in terms of $W$, the maximum force that can be applied without causing the cylinder to rotate.

A trailer with loaded weight $F_g$ is being pulled by a vehicle with a force $P$, as in figure. The trailer is loaded such that its centre of mass is located as shown. Neglect the force of rolling friction and let a represent the $x$ component of the acceleration of the trailer.
(a) Find the vertical component of $P$ in terms of the given parameters.

(b) If $a=2.00{ \mathrm{ms}}^{-2}$ and $h=1.50 \mathrm{m},$, what must be the value of $d$ in order that $P_y=0$ (no vertical load on the vehicle)?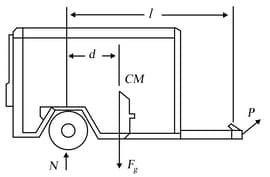

A uniform cube of side $a$ and mass $m$ rests on a rough horizontal table. A horizontal force $F$ is applied normal to one of the faces at a point directly above the centre of the face, at a height $3a/4$ above the base. What is the minimum value of $F$ for which the cube begins to tip about an edge?

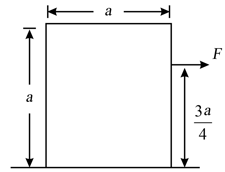
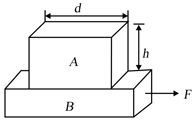
A rectangular block ‘ $A$’ having height $h$ and width $b$ has been placed on another block $B$ as shown in the figure. Both blocks have equal mass and there is no friction between the block ‘ $B$’ and ground. A horizontal time dependent force; $F=kt$ is applied on the block ‘ $B$’ At what time will block ‘ $A$’ topple? Assume that friction between the two blocks is large enough to prevent the block ‘ $A$’ from slipping.

A tall block of mass $M=50 \mathrm{kg}$ and base width $b=1 \mathrm{m}$ and height $h=3 \mathrm{m}$ is kept on a rough inclined surface with coefficient of friction $\mu =0.8$ as shown in figure. The

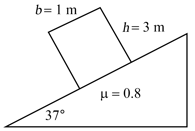
angle of inclination with the horizontal is ${37}^{\mathrm{o}}$. Determine whether the block slides down or topples over.

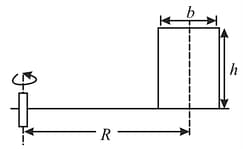
A rectangular block rests on a horizontal rotating disc, as shown in the figure. Find at what angular velocity $\omega$, the block falls of the disc, if the distance between the axis of the disc and block is $R$ and the coefficient of friction $\mu >\frac{b}{h},$ where $b$ is the width of the block and $h$ is its height.

A uniform rod of mass m and length $l$ can rotate in a vertical plane about a smooth horizontal axis hinged at point $H$.

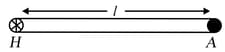
(a) Find angular acceleration $\alpha$ of the rod just after it is released from initial horizontal position from rest?

(b) Calculate the acceleration (tangential and radial) of point $A$ at this moment.