The magnetic energy density of a solenoid is independent of magnetic permeability in vacuum.

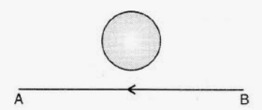
The electric current flowing in a wire in the direction from B to A is decreasing. Find out the direction of the induced current in the metallic loop kept above the wire as shown.

What is the magnetic energy stored in the solenoid? How does this magnetic energy compare with the electrostatic energy stored in a capacitor?

A coil $Q$ is connected to low voltage bulb $B$ and placed near another coil $P$ as shown in Fig. 6.74. Give reasons to explain the following observation:

The bulb '$B$' lights.

A $50 \mathrm{mH}$ coil carries a current of $2 \mathrm{A}$, the energy stored in joule is

A conducting wire $\mathrm{XY}$ of mass $m$ and neglibile resistance slides smoothly on two parallel conducting wires as shown in Figure. The closed circuit has a resistance $R$ due to $\mathrm{AC}, \mathrm{AB}$ and $\mathrm{CD}$ are perfect conductors. There is a magnetic field $\mathrm{B}=\mathrm{B}\left(\mathrm{t}\right)\hat{\mathrm{k}}$.

For (b), show that the decrease in kinetic energy of $\mathrm{XY}$ equals the heat lost in $R$.