The ground state energy of hydrogen atom is - 13.6 e V . Consider an electronic state Ψ of H e + whose energy, azimuthal quantum number and magnetic quantum number are - 3.4 e V , 2 and 0 respectively. Which of the following statement(s) is(are) true for the state Ψ ?

The nuclear charge experienced by the electron in this state is less than 2 e , where e is the magnitude of the electronic charge.

EASY

JEE Main/Advanced

IMPORTANT

Earn 100

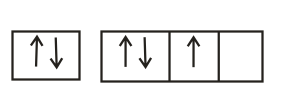
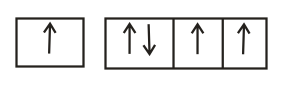
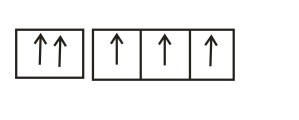
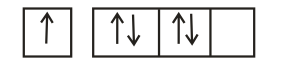
The orbital diagram in which Hund's rule and Aufbau principle is violated is

50% studentsanswered this correctly

Important Points to Remember in Chapter -1 - Structure of Atom from Embibe Experts Gamma Question Bank for Engineering Chemistry Solutions

1. Discovery of Subatomic Particles:

(i) Discovery & their discoverers:

Name of Particles	Scientist
Electron	J.J. Thomson
Proton	Goldstein
Neutron	Chadwick
Cathode Ray	William Crookes
Anode Ray	Goldstein
Nucleus	Rutherford
Atomic No.	Moseley
Nomenclature of $e^{-}$	Stoney
Charge of $e^{-}$	Millikan
Specific charge on $e^{-} (e / m)$	J.J. Thomson

(ii) Properties of the three main subatomic particles:

Name	Electron	Proton	Neutron
Symbol	e	p	n
Absolute charge	$- 1.6022 \times 10^{- 19} C$	$+ 1.6022 \times 10^{- 19} C$	$0$
Relative Electric charge	$- 1$	$+ 1$	$0$
Mass $(k g)$	$9.10939 \times 10^{- 31}$	$1.67262 \times 10^{- 27}$	$1.67493 \times 10^{- 27}$
Molar Mass $(g)$	$0.00054$	$1.00727$	$1.00867$
Approximate mass(u)	$0$	$1$	$1$

2. Atomic number, Mass number and the Atomic species:

(i) Atomic number $(Z) =$ number of protons.

Mosely's relation $\Rightarrow \sqrt{v} = a (z - b)$ .

(ii) Mass number $(A) =$ number of $(n + p)$ .

(iii) Isotopes $=$ Same $Z$ but different $A$ .

(iv) Average atomic weight

$= \frac{m_{1} x_{1} + m_{2} x_{2} + m_{3} x_{3} + \dots \dots \dots}{x_{1} + x_{2} + x_{3} + \dots \dots \dots . .}$

, where $m_{1}, m_{2}, m_{3}$ are mass of the isotopes and

$x_{1}, x_{2}, x_{3}$ are their percentage abundance or relative ratio.

(v) Isobars $=$ Same $A b u t$ different $Z$ .

(vi) Isotones/Isoneutronic $=$ same number of neutrons.

(vii)Isodiapheres $=$ Same $(n - p)$

(viii)Isosteres $=$ Molecules with the same number of atoms and electrons.

(ix) Isoelectronic $=$ Same number of electrons.

3. Atomic Models:

(i) Thomson Model of an atom:

J. J. Thomson, in $1898$ , proposed that an atom possesses a spherical shape (radius approximately $10^{- 10} m$ ) in which the positive charge is uniformly distributed. The electrons are embedded into it in such a manner as to give the most stable electrostatic arrangement. Many different names are given to this model, for example, plum pudding, raisin pudding or watermelon.

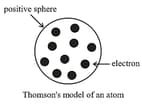
Question Image

Limitation: This model was able to explain the overall neutrality of the atom but was not consistent with the results of later experiments.

(ii) Rutherford’s alpha particle scattering experiment and model:

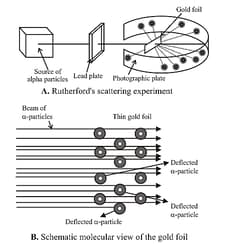
Question Image

Observations:

(a) most of the $α$ – particles passed through the gold foil were undeflected.

(b) a small fraction of the $α$ –particles was deflected by small angles.

Conclusions:

(a) Most of the space in the atom is empty as most of the $α$ –particles passed through the foil undeflected.

(b) A few positively charged $α$ – particles were deflected. The deflection must be due to the enormous repulsive force showing that the positive charge of the atom is not spread throughout the atom as Thomson had presumed. The positive charge has to be concentrated in a very small volume that repelled and deflected the positively charged $α$ – particles.

(c) Calculations by Rutherford showed that the volume occupied by the nucleus is negligibly small as compared to the total volume of the atom. The radius of the atom is about $10^{- 10} m$ , while that of the nucleus is $10^{- 15} m$ .

Rutherford proposed the nuclear model of atoms (after the discovery of protons):

(d) The positive charge and most of the mass of the atom was densely concentrated in an extremely small region. This very small portion of the atom was called the nucleus by Rutherford.

(iii) The nucleus is surrounded by electrons that move around the nucleus with a very high speed in circular paths called orbits. Thus, Rutherford’s model of atom resembles the solar system in which the nucleus plays the role of the sun and the electrons of the revolving planets.

(iv) Electrons and the nucleus are held together by electrostatic forces of attraction.

Estimation of the closest distance of approach (derivation).

An $α -$ particle is projected from infinity with a velocity $V_{0}$ towards the nucleus of an atom having the atomic number equal to $Z$ , then find out (i) the closest distance of approach $(R)$ , (ii) what is the velocity of the $α$ -particle at the distance $R_{1} (R_{1} > R)$ from the nucleus.

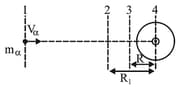
Question Image

From energy conservation, $P . E_{1} + {K E}_{1} = {P . E}_{2} + {K E}_{2}$

$\Rightarrow 0 + \frac{1}{2} m_{α} V_{α}^{2} = \frac{K (Ze) (2 e)}{R} + 0$

$R = \frac{4 K Z e^{2}}{m_{α} V_{α}^{2}}$ (the closest distance of approach)

Let velocity at $R_{1}$ is $V_{1}$

From energy conservation, ${P . E}_{1} + {K E}_{1} = P . E_{3} + {K E}_{3}$

$\Rightarrow 0 + \frac{1}{2} m_{α} V_{α}^{2} = \frac{K (Ze) (2 e)}{R_{1}} + \frac{1}{2} m_{α} V_{1}^{2}$

4. Size of the Nucleus:

The volume of the nucleus is very small and is only a minute fraction of the total volume of the atom. Nucleus has a diameter of the order of $10^{- 12}$ to $10^{- 13} c m$ and the atom has a diameter of the order of $10^{- 8} c m .$ Thus, diameter (size) of the atom is $100,000$ times the diameter of the nucleus.

The radius of a nucleus is proportional to the cube root of the number of nucleons within it.

$R = R_{0} {(A)}^{\frac{1}{3}} c m$

Where $R_{0}$ can be $1.1 \times 10^{- 13} t o 1.44 \times 10^{- 13} c m; A =$ mass number; $R =$ Radius of the nucleus.

Nucleus contains protons and neutrons except hydrogen atoms, which does not contain neutrons in the nucleus.

5. Wave Nature of Electromagnetic Radiation:

Electromagnetic wave radiation:

The oscillating electrical/magnetic field are electromagnetic radiations. Experimentally, the direction of the oscillations of the electrical and the magnetic field are perpendicular to each other.

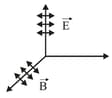
Question Image

$\vec{E} = E l e c t r i c f i e l d, \vec{B} = M a g n e t i c f i e l d$

Question Image

Direction of the wave propagation.

Some important characteristics of a wave:

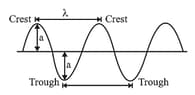
Question Image

Wavelength of a wave is defined as the distance between any two consecutive crests or troughs. It is

represented by $λ$ (lambda) and is expressed in $\dot{A}$ or $m$ or $c m$ or $n m$ (nanometer) or $p m$ (picometer).

$1 Å = 10^{- 8} c m = 10^{- 10} m$

$1 n m = 10^{- 9} m, 1 p m = 10^{- 12} m$

Frequency of a wave is defined as the number of waves passing through a point in one second. It is

represented by $ν (nu)$ and is expressed in $H e r t z (Hz)$ or $c y c l e s / s e c$ or simply ${s e c}^{- 1}$ or $s^{- 1} .$

$1 H z = 1 c y c l e / s e c$

Velocity of a wave is defined as the linear distance travelled by the wave in one second. It is represented by $v$ and is expressed in $c m / s e c$ or $m / s e c ({m s}^{- 1})$ .

Amplitude of a wave is the height of the crest or the depth of the trough. It is represented by $' a'$ and is

expressed in the units of length.

Wave number is defined as the number of waves present in $1 c m$ length. Evidently, it will be equal to the reciprocal of the wavelength. It is represented by $\bar{υ}$ (read as $n u$ bar).

$\bar{υ} = \frac{1}{λ}$

If $λ$ is expressed in $cm, \bar{ν}$ will have the units ${c m}^{- 1} .$

The relationship between the velocity, the wavelength, and the frequency of a wave. As the frequency is the number of waves passing through a point per second and $λ$ is the length of each wave, hence, their product will give the velocity of the wave. Thus, $c = ν \times λ$ .

6. Spectrum:

(i) Electromagnetic Spectrum:

The arrangement of various types of electromagnetic radiations in the order of their increasing or decreasing wavelength or frequency is known as electromagnetic spectrum.

Radiation	Wavelength $(A)$	Frequency $(H z)$
Gamma rays	$0.01$ to $0.1$	$3 \times 10^{19}$ to $3 \times 10^{20}$
X-rays	$0.1$ to $150$	$2 \times 10^{16}$ to $3 \times 10^{19}$
UV radiations	$150$ to $3800$	$7.9 \times 10^{14}$ to $2 \times 10^{16}$
Visible rays	$3800$ to $7600$	$3.95 \times 10^{14}$ to $7.9 \times 10^{14}$
Microwaves	$6 \times 10^{6}$ to $3 \times 10^{9}$	$1 \times 10^{5}$ to $1 \times 10^{9}$

(ii) Order of wavelength in electromagnetic spectrum:

cosmic rays $< γ -$ rays $< X -$ rays $<$ Ultraviolet rays $<$ Visible $<$ Infrared $<$ Microwaves $<$ Radio waves.

(iii) Spectrum (Important points):

Continuous emission spectrum is given by incandescent sources.

Emission line spectrum is given by atoms.

Emission band spectrum is given by molecules.

Angle of deviation $\propto$ frequency of radiation:

More lines are observed in the emission spectrum than the absorption spectrum.

Hydrogen Spectrum $(n_{2} \to n_{1})$
Lyman $⟶$ Any higher orbit $⟶ 1$	[Found in $U . V .$ region]
Balmer $⟶$ Any higher orbit $⟶ 2$	[Found in Visible region]
Paschen $\to$ Any higher orbit $⟶ 3$	[Found in $I . R .$ region]
Brackett $\to$ Any higher orbit $⟶ 4$	[Found in $I . R .$ region]
$P$ fund $⟶$ Any higher orbit $⟶ 5$	[Found in $I . R .$ region]

7. Rydberg Equation:

Wave number $= \frac{1}{λ} = R_{H} Z^{2} (\frac{1}{n_{1}^{2}} - \frac{1}{n_{2}^{2}})$

Wave number $= R_{H} {CZ}^{2} (\frac{1}{n_{1}^{2}} - \frac{1}{n_{2}^{2}})$

$E = R_{H} C Z^{2} h (\frac{1}{n_{1}^{2}} - \frac{1}{n_{2}^{2}})$

Where $C =$ the velocity of the electromagnetic waves.

Where $R_{H} =$ Rydberg constant $= 109678 {c m}^{- 1}$

$= 10967800 m^{- 1}$ .

$\frac{1}{R_{H}} = 912 Å$

$R_{H} C h =$ Energy of the $I^{s t}$ orbit of hydrogen.

$R_{H} C h Z^{2} =$ Energy of the Ist orbit of any hydrogen-like species.

Important points:

(i) $α$ line/First line/Starting line/Initial line (First line of any series).

(ii) Last line/Limiting line/Marginal line (Last line of any series).

(iii) Total number of lines in the emission spectrum for $(n_{2} \to n_{1})$ .

$(T . E . L)$ Total emission lines But for $= \frac{(n_{2} - n_{1}) (n_{2} - n_{1} + 1)}{2}$

$(n \to 1), T . E . L = \frac{n (n - 1)}{2}$

8. Particle Nature of Electromagnetic Radiation:

Particle Nature of Electromagnetic Radiation: Planck's Quantum Theory

Some of the experimental phenomenon such as diffraction and interference can be explained by the wave nature of the electromagnetic radiation. However, following are some of the observations which could not be explained.

(i) The nature of the emission of radiation from hot bodies (black - body radiation).

(ii) The ejection of electrons from metal surface when radiation strikes it (photoelectric effect).

Black Body Radiation:

When solids are heated, they emit radiation over a wide range of wavelengths. The ideal body, which emits and absorbs all frequencies, is called a black body and the radiation emitted by such a body is called the black body radiation. The exact frequency distribution of the emitted radiation (i.e., intensity versus frequency curve of the radiation) from a black body depends only on its temperature.

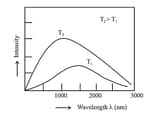
Question Image

The above experimental results cannot be explained satisfactorily on the basis of the wave theory of light.

Planck suggested that atoms and molecules could emit (or absorb) energy only in discrete quantities and not in a continuous manner.

9. Quantum Theory of Light:

The smallest quantity of energy that can be emitted or absorbed in the form of electromagnetic radiation is called as quantum of light.

According to Planck, the light energy coming out from any source is always an integral multiple of a smallest energy value called quantum of light.

Let quantum of light be $= E_{0}$ , then total energy coming out is $= n E_{0}$ ( $n =$ Integer).

Quantum of light $=$ Photon (Packet or bundle of energy).

Energy of one photon is given by:

$E_{0} = hν (ν = Frequency of light)$

$h = 6.625 \times 10^{- 34} J . s e c (h = planck' s constant)$

$E_{0} = \frac{hc}{λ} (c = speed of light)$

$(λ = wavelength)$

Order of magnitude of $E_{0} = \frac{10^{- 34} \times 10^{8}}{10^{- 10}} = 10^{- 16} J$

One electron volt $(eV)$ : The energy gained by an electron when it is accelerated from rest through a potential difference of $1$ volt.

Note: Positive charge always moves from a high potential to a low potential and $- v e$ charge always moves from a low potential to a high potential if set free.

If a charge $' q'$ is accelerated through a potential difference of $" V'$ volt, its kinetic energy will be increased by $q V .$

$1 e V = 1.6 \times 10^{- 19} C \times 1 v o l t$

$∴ 1 e V = 1.6 \times 10^{- 19} J$

10. Photoelectric Effect:

When certain metals (for example Potassium, Rubidium, Cesium etc.) were exposed to a beam of light, the electrons were ejected as shown in the figure:

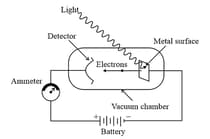
Question Image

The phenomenon is called Photoelectric effect. The results observed in this experiment were:

(i) The electrons are ejected from the metal surface as soon as the beam of light strikes the surface, i.e., there is no time lag between the striking of light beam and the ejection of electrons from the metal surface.

(ii) The number of electrons ejected is proportional to the intensity or brightness of light.

(iii) For each metal, there is a characteristic minimum frequency $υ_{o}$ (also known as threshold frequency) below which photoelectric effect is not observed. At a frequency $υ > υ_{o},$ the ejected electrons come out with a certain kinetic energy. The kinetic energies of these electrons increase with the increase of frequency of the light used.

The kinetic energy of the ejected electron is given by the equation:

$h υ = {h υ}_{0} + \frac{1}{2} m_{e} v^{2}$ , where $m_{e}$ is the mass of the electron and $v$ is the velocity associated with the ejected electron.

11. Bohr's Model for the Hydrogen Atom:

(i) Applicable for single electron species only, like $H, {H e}^{+}, {L i}^{+ 2}, {B e}^{+ 3}, {N a}^{+ 10}$ , etc.

(ii) Related with the particle nature of electron.

(iii) Based on Planck’s quantum theory.

Important Formulae:

(a) Angular momentum in an orbit is quantized.

$m v r = n \times \frac{h}{2 π}$

(b) Radius of Bohr orbit $= r = \frac{n^{2} h^{2}}{4 π^{2} {m K Z e}^{2}}$

On solving $r = 0.529 \times \frac{n^{2}}{Z} Å$ , where $0.529 Å = a_{0}$ is called the atomic unit of length (Bohr).

$v = \frac{2 π {K Z e}^{2}}{n h}$

On solving $v = 2.18 \times 10^{6} \frac{Z}{n} m / s$

$v = 2.18 \times 10^{8} \frac{Z}{n} c m / s$

(d) Energy of an electron in Bohr orbit:

Potential Energy $(PE) = - \frac{K Z e^{2}}{r}$ i.e., At $r = \infty, P E = 0$

Kinetic Energy $(K E) = \frac{1}{2} \frac{{K Z e}^{2}}{r}$ i.e., At $r = \infty, K E = 0$

Total Energy $(T E) = - \frac{2 π^{2} {m K}^{2} Z^{2} e^{4}}{n^{2} h^{2}}$

On solving $T E = - 2.18 \times 10^{- 18} \times \frac{Z^{2}}{n^{2}} J / a t o m$

$= - 13.6 \times \frac{Z^{2}}{n^{2}} e V / a t o m$

$= - 313.6 \times \frac{Z^{2}}{n^{2}} K c a l / m o l$

$= - 1313.6 \times \frac{Z^{2}}{n^{2}} K J / m o l$

"Relation between " $T E, P E$ and $K E$

$\Rightarrow P E = 2 \times T E$

$\Rightarrow T E = - K E$

$\Rightarrow P E = - 2 K E$

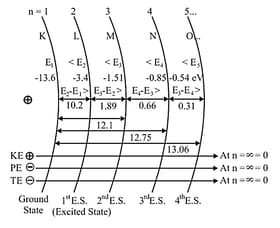
Question Image

Important Shortcuts:

$T . E$ of any $H -$ like species $= T E$ of Hydrogen $\times Z^{2}$

(For same orbit)

$Δ E$ for $H -$ like species $= Δ E$ (For Hydrogen) $\times Z^{2}$

(For same transition)

Energy in $n^{t h}$ orbit-for $H$ like species $= \frac{E_{1}}{n^{2}}$ [For same atom]

$(I . E .)$ "ionization Energy $\Rightarrow n = 1 ⟶ n = \infty$

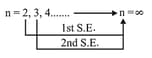
(S.E.) Separation Energy

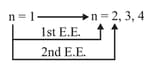
Question Image

(E.E) Excitation Energy $=$

Question Image

(iv) Failures / limitations of Bohr's theory:

(a) He could not explain the line spectra of atoms containing more than one electron.

(b) He also could not explain the presence of multiple spectral lines.

(c) He was unable to explain the splitting of spectral lines in magnetic field (Zeeman effect) and in electric field (Stark effect).

(d) No conclusion was given for the principle of quantization of angular momentum.

(e) He was unable to explain the de-Broglie's concept of the dual nature of matter.

(f) He could not explain Heisenberg's uncertainty principle.

12. Towards Quantum Mechanical Model of atom:

(i) Dual nature of electron (de-Broglie Hypothesis):

(a) Einstein had suggested that light can behave as a wave as well as like a particle, i.e., it has a dual character.

(b) In $1924,$ de-Broglie proposed that an electron behaves both as a material particle and as a wave.

(c) This proposed a new theory called the wave mechanical theory of matter. According to this theory, the electrons protons and even atoms, when in motion, possess wave properties.

(d) According to de-Broglie, the wavelength associated with a particle of mass $m,$ moving with a velocity $v$ , is given by the relation,

$λ = \frac{h}{m v}$ , where $h$ is Planck's constant.

$λ = \frac{h}{\sqrt{2 m K E}}$

$m = m a s s$

$v = v e l o c i t y$

$K E =$ Kinetic Energy

$V = P o t e n t i a l$

$λ = \frac{h}{\sqrt{2 m q V}}$ for electron if solved, then $λ = \sqrt{\frac{150}{V}} \dot{A}$

(ii) de-Broglie’s explanation for Bohr’s model:

$m v r = n \times \frac{h}{2 π}$

$λ = \frac{h}{m v}$

$m v = \frac{h}{λ}$ putting this in $m v r = \frac{n h}{2 π}$

$∴ \frac{h}{λ} r = \frac{n h}{2 π}$

$\Rightarrow [λ = \frac{2 π r}{n}]$ de Broglie wavelength

(iii) Important Points:

(a) When an $e^{-}$ revolves in orbit then no. of waves made by $e^{-} =$ orbit number $(n) .$

(b) Frequency of matter waves.

$υ = \frac{v}{λ} = \frac{v P}{h} = \frac{m v^{2}}{h} = \frac{2 K E}{h} [υ = frequency]$

13. Heisenberg's Uncertainty Principle:

The exact position and momentum of a fast-moving particle cannot be calculated precisely at the same

moment of time. If $Δ x$ is the error in the measurement of the position of the particle and if $Δ p$ is the error in the measurement of momentum of the particle, then:

$Δ x, Δ p \geq \frac{h}{4 π}$ or $Δ x \cdot (mΔv) \geq \frac{h}{4 π}$

, where $Δ x =$ uncertainty in the position

$Δ p =$ uncertainty in the momentum

$h =$ Plank's constant

$m =$ mass of the particle

$Δ v =$ uncertainty in the velocity

$\frac{h}{4 π} = 5.27 \times 10^{- 35} J . s e c .$ (In SI unit)

14. Quantum Mechanical Model of atom:

Orbital Wave Functions, Probability Distribution and Shape of Orbitals:

(i) Wave function $(ψ)$ provides useful information about an electron. These are:

(a) Energy of the electron in an orbital.

(b) Position of the electron in space in a particular allowed energy state.

(ii) On the basis of values of ${|ψ|}^{2},$ i.e., the probability of finding electron, electron clouds may be drawn and the region where they are dense shows the region of high probability.

(iii) The plane and the point where $| ψ |^{2}$ is zero (i.e., no probability) are called nodal plane or nodal point, respectively.

(iv) Orbital wave function $ψ$ is the product of two functions: radial function and angular function, i.e.,

$ψ = ψ_{(r)}, ψ_{(ω)}$

$ψ_{(r)}$ is the function of the distance $(r)$ from the nucleus while $ψ_{(ω)}$ is the function of the two spherical co-ordinates $θ$ and $ϕ$ as shown in figure:

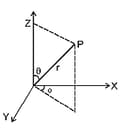
Question Image

(v) $ψ_{(r)}$ , i.e., the radial part of the wave function depends upon the quantum number $n$ and $l$ and decides the size of an orbital.

(vi) The angular part of the wave function $ψ_{(ω)},$ depends upon the quantum numbers $l$ and $m$ and describes the shape of orbital.

For the sake of convenience, the $ψ_{(r)} vs . r$ and $ψ_{(ω)} vs$ . angle are plotted separately.

15. Orbital:

An orbital may be defined as the region of space around the nucleus where the probability of finding an electron is maximum $(90 % to 95 %) .$

Orbitals do not define a definite path for the electron, rather they define only the probability of the electron being in various regions of space around the nucleus.

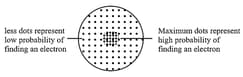
Question Image

(i) The s-orbitals:

(a) All the $s$ -orbitals are spherical and show spherical symmetry. Being symmetrical, they do not have directional dependence.

(b) The size (or radii) of $s -$ orbital depends upon the value of $n$ and increases in proportionality of $n^{2} .$

(ii) The $p$ -orbitals:

(a) $p$ -orbitals are not spherically symmetrical and have dumb-bell shape.

(b) $p -$ subshell is constituted by three $p$ -orbitals $p_{x^{}}, p_{y}$ and $p_{z}$ named with respect to the axis.

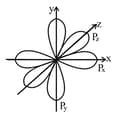
Question Image

Figure: Electron-density distribution in a $2 p -$ orbital

(d) For a $p$ -orbital to exist, minimum values of $n = 2,$ because for $p -$ subshell $l = 1,$ and the minimum value of $n$ which gives $l = 1$ is $2 .$ Thus, $1 p -$ orbital does not exist, and they start from $2 p$ .

(e) For $l = 1$ value of $m = - 1, 0, + 1$ and each other of $m$ indicates one $p -$ orbital. e.g., $2 p -$ subshell contains $2 p_{x^{'}} 2 p_{y^{'}}$ and $2 p_{z}$ orbitals.

All the three have the same shape and energy (i.e., degenerate) and differ in orientation only.

The wave function for $p_{z}$ has maximum amplitude along $z -$ axis. It is zero along $x y$ plane. Similarly, $p_{x}$ and $p_{y}$ has the maximum probability of finding electron along $x$ and $y -$ axis.

(iii) The $d$ -orbitals:

(a) For $d -$ subshell, value of $l = 2$ and minimum value of $n,$ which gives $l = 2,$ is $3 .$ Thus, $1 d$ or $2 d -$ orbitals have no existence, and they start from $3 d .$

(b) For $l = 2,$ the values of $m = - 2, - 1, 0, + 1, + 2,$ (five values), thus, each $d -$ subshell is made up of five $d -$ orbitals which are $d_{x y^{'}} d_{y z}, d_{z x^{}}, d_{x^{2} - y^{2}}, d_{z^{2}}$ .

(c) Except $d_{z^{2}},$ they have four lobes separated by a node (nucleus) while $d_{z^{2}}$ has only two lobes. Their shapes have been shown below:

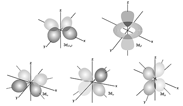
Question Image

(d) Lobes of $d_{x y^{'}} d_{y z}$ and $d_{z x}$ lie between the axis, while $d_{x^{2} - y^{2}}$ and $d_{z^{2}}$ lie on the axis.

(e) $d_{z^{2}}$ has two lobes on $z -$ axis and doughnut in $x y -$ plane. It looks like a baby soother.

(f) All the $d$ -orbitals belonging to a subshell have same energy and so are degenerate (fivefold degeneracy).

(iv) The $f$ -orbitals:

(a) For $f -$ subshell $l = 3$ and thus $m$ will have seven values $m = - 3, - 2, - 1, 0, + 1, + 2, + 3 .$ For $l = 3,$ minimum value of $n$ must be four thus 1f, $2 f$ of $3 f$ have no existence and $f -$ orbitals start from $n = 4 (i . e ., 4 f) .$

(b) In a $f -$ subshell, there are seven $f -$ orbitals. Their contour diagram which are $3 - D$ , are difficult to draw on a paper.

(c) The seven f-orbitals are: $f_{x (x^{2} - y^{2})}, f_{y (x^{2} - y^{2})}, f_{z (x^{2} - y^{2})}, f_{x y z}, f_{z^{3}}, f_{y z^{2}}$ and $f_{x z^{2}}$ .

Note:

(a) Sometimes, an orbital is represented in terms of $ψ_{n, l, m}$ also. Usually for $m = 0, z -$ axis is chosen.

e.g., $ψ_{420}$ reveals that $n = 4, l = 2$ and $m = 0,$ thus it is $4 d_{z^{2}}$ .

(b) For an orbital (or subshell), as the value of n increases, the size of the orbital increases, i.e., $1 s < 2 s < 3 s$ , etc.

(c) As $r$ approaches to $0, ψ$ also approaches zero except $s -$ orbital. It concludes that only $s -$ electron can penetrate through nucleus and has the probability to be found at the nucleus.

(d) For one electron system (e.g., $H^{+}, {L i}^{2 +}, {B e}^{3 +} e t c .),$ the energy of the orbital depends only on the value of $n$ and not on $l$ . Thus, all the subshells belonging to same shell will have the same energy.

(e) There is no unique way of representing the angular dependence functions of all seven $f$ -orbitals. An

alternative way may be as $f_{z^{3}}, f_{x z^{2}}, f_{y x^{2}}, f_{z y^{2}}, f_{x (x^{2} - 3 y^{2})}, f_{y (y^{2} - 3 z^{2})}$ and $f_{z {(z^{2} - 3 x^{2})}^{*}}$ .

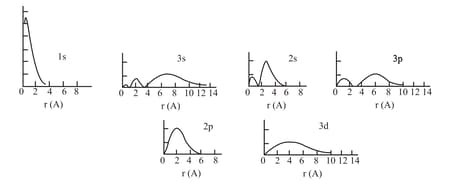
Question Image

The radial probability density for some orbitals of the hydrogen atom. Ordinate is proportional to

$4 π r^{2} R^{2},$ and all distributions are to the same scale.

16. Node and Nodal Plane:

(i) Node represents the region where probability of finding an electron is zero (i.e., $ψ$ and $ψ^{2} = 0$ ). Similarly, nodal plane represents the plane having zero probability of finding an electron.

(ii) Nodes are of two types:

(a) Radial node

(b) Angular node

A radial node is the spherical region around nucleus having $ψ$ and $ψ^{2}$ equal to zero. An orbital having a higher number of nodes has more energy.

(iii) Calculation of the number of nodes:

Radial nodes $= n - l - 1$

Angular nodes $= l$

Total nodes $= n - 1$

$n$ and $l$ are principal and azimuthal quantum numbers. e.g., in $3 p -$ orbital.

Radial nodes $= 3 - 1 - 1 = 1 (= n - l - 1)$

Angular nodes $= 1 (= l)$

Total nodes $= 2$ (one radial, one angular)

(iv) For one electron system, the energy depends only upon the number of nodes $(n - 1)$ and not upon the types of nodes.

17. Degenerate and Non-degenerate Orbitals:

Orbitals belonging to the same subshell and having the same energy are known as degenerate orbitals. Degeneracy is maintained in the absence of a magnetic field but destroyed if the degenerate orbitals are kept in the magnetic field. Thus,

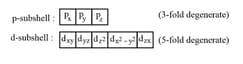
Question Image

18. Quantum Numbers:

The set of four integers required to define the state of an electron in an atom are called quantum numbers. The quantum numbers are:

(i) Principal quantum number $(n)$ .

(ii) Azimuthal quantum number $(l) .$

(iii) Magnetic quantum number $(m) .$

(iv) Spin quantum number $(s)$ .

(a) Principal quantum number, $(n)$ , relates to the amplitude (i.e., size) of an electron wave and also the total energy of the electron. It has integral values of $1, 2, 3, 4, \dots$ etc., also denoted as $K, L, M, N \dots .$ etc.

(b) Azimuthal quantum number $(l)$ , tells us about the sub-energy shell of an electron. For each main energy shell, there can be $' n'$ number of sub-energy shells. These sub-energy shells are designated by different values of $l .$ For each value of $n, l$ can have the values from $0, 1, 2, 3 \dots n - 1 .$

(c) Magnetic quantum number, $(m),$ explains the behavior of an electron in the external magnetic field or in other words, it tells us about orbitals of the electrons. The values of $m$ gives the number of orbitals associated with a particular sub-shell in the shell. For each value of $l, m$ can have values from $- l$ to $+ l$ including zero.

e.g., when $l = 1, m = - 1, 0, + 1; l = 2, m = - 2, - 1, 0, + 1, + 2$

(d) Spin quantum number, $(s)$ , Each spinning electron can have two values of s = $+ \frac{1}{2}$ or $- \frac{1}{2}$

19. Filling of Electrons in Orbitals:

(i) Rules for filling of orbitals:

(a) Aufbau principle: The electrons are filled up in the increasing order of the energy in sub-shells.

$1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 4 s^{2} 3 d^{10} 4 p^{6} 5 s^{2} 4 d^{10} 5 p^{6} 6 s^{2} 4 f^{14} 5 d^{10} 6 p^{6} 7 s^{2} 5 f^{14} 6 d^{10}$ .

(b) $(n + l)$ rule: The sub-shell with the lowest $(n + l)$ value is filled up first, but when two or more sub-shells have the same $(n + l)$ value, the sub-shell with the lowest value of $n$ is filled up first.

(c) Pauli exclusion principle: Pauli stated that no two electrons in an atom can have the same values of all four quantum numbers.

(d) Hund's rule of maximum multiplicity: Electrons are distributed among the orbitals of a sub-shell in such a way as to give maximum number of unpaired electrons with parallel spin.

(ii) Exceptions:

(a) $_{24} C r = [Ar] 4 s^{2}, 3 d^{4}$ (Not correct)

$[A r] 4 s^{1}, 3 d^{5}$ (correct: as $d^{5}$ structure is more stable than $d^{4}$ structure)

(b) $_{29} C u = [Ar] 4 s^{1}, 3 d^{10} (c o r r e c t : a s d^{10} s t r u c t u r e i s m o r e s t a b l e t h a n d^{9} s t r u c t u r e)$

The orbital diagram in which Hund's rule and Aufbau principle is violated is

Important Points to Remember in Chapter -1 - Structure of Atom from Embibe Experts Gamma Question Bank for Engineering Chemistry Solutions

Learn and Prepare for any exam you want !