The relation between angular acceleration and tangential acceleration is given as

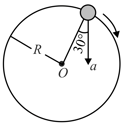
In the given figure, $a=15 \mathrm{m} {\mathrm{s}}^{-2}$ represents the total acceleration of a particle moving in the clockwise direction in a circle of the radius $R=2.5 \mathrm{m}$at a given instant of time. The speed of the particle is

A stone tied to $180 \mathrm{cm}$ long string at its end is making $28$ revolutions in horizontal circle in every minute. The magnitude of acceleration of stone is $\frac{1936}{x} \mathrm{m} {\mathrm{s}}^{-2}$. The value of $x$ ______.

[Take $\pi =\frac{22}{7}$]

If the kinetic energy of a particle of mass $m,$ performing uniform circular motion in a circle of radius $r,$ is $E,$ find the acceleration of the particle.