The spherical ring shown below is created by drilling a cylindrical hole through a sphere in such a way that the centres of the cylindrical hole and the sphere coincide.The radius of the spherical ring is 15 cm and length of hole drilled through the sphere is 18 cm.

 

The volume of the spherical cap (part shaded in yellow in the figure) of height ‘h’, is$ {\text{V}}_{\text{cap}}$ = $ \frac{1}{3}$π$ {h}^{2}$(3R – h), where ‘R’ is the radius of the spherical ring.

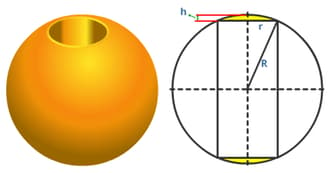
The volume the ring is cc.

(Note: Use π = 3.14 and round your answer to the nearest whole number.)

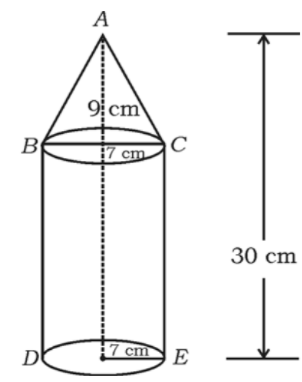
A solid is in the form of a cone mounted on a right circular cylinder, both having same radii as shown in the figure. The radius of the base and height of the cone are $7 \mathrm{cm}$ and $9 \mathrm{cm}$ respectively. If the total height of the solid is $30 \mathrm{cm}$, find the volume of the solid.

The picture shows the shape of a boiler. Total height of the boiler is $12$ metres and the diameter is $6$ meters, height of the cylindrical part is $6$ meters.

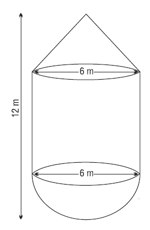
How many litres can the boiler hold ?

($1 m^3=1000$ litre)

If a cubical container of length, breadth and height each of $10 \mathrm{cm}$ can contain exactly $1$ litre of water, then a spherical container of radius $10.5 \mathrm{cm}$ can contain

The perimeter and the breadth of a rectangle are $52 cm$ and $12 cm$ respectively. Find its area in $c{m}^2$.

If a hemisphere is melted and four spheres of equal volume are made, the radius of each sphere will be equal to.

The length and breadth of a rectangular sheet are 48 m and 36 m respectively. A square is cut off from each of its corners, so that an open box be made. If the side of square be 16m, what will be the volume of the box so formed (in cubic m)? 

(A) 1,024 

(B) 1,224 

(C) 1,324 

(D) 1,124