Let f x be a non-constant polynomial with real coefficients such that f 1 2 = 100 & f x ≤ 100 for all real x . Which of the following statements is NOT necessarily true?

The coefficient of the highest degree term in f x is negative

f x has at least two real roots

At least one of the coefficients of f x is bigger than 50

MEDIUM

Earn 100

The sum of an infinite geometric series is $162$ and sum of its first $n$ terms is $160 .$ If the inverse of common ratio $r$ is an integer, then which of the following option $(s)$ are correct?

50% studentsanswered this correctly

Important Questions on Seeing Structure in Expressions

MEDIUM

Mathematics>Algebra>Seeing Structure in Expressions>Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems.

Suppose

p, q, r

are real numbers such that

q = p (4 - p), r = q (4 - q), p = r (4 - r) .

The maximum possible value of

p + q + r

MEDIUM

Mathematics>Algebra>Seeing Structure in Expressions>Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems.

The sum of the

3^{r d}

and the

4^{t h}

terms of a

G . P .

60

and the product of its first three terms is

1000.

If the first term of this

G . P .

is positive, then its

7^{t h}

term is:

MEDIUM

Mathematics>Algebra>Seeing Structure in Expressions>Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems.

The quotient when

1 + x^{2} + x^{4} + . . . + x^{34}

is divided by

1 + x + x^{2} + . . . + x^{17}

MEDIUM

Mathematics>Algebra>Seeing Structure in Expressions>Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems.

Let

f : x \to y

be such that

f (1) = 2

and

f (x + y) = f (x) f (y)

for all natural numbers

x

and

y

.

\sum_{k = 1}^{n} f (a + k) = 16 (2^{n} - 1)

then

a

is equal to

HARD

Mathematics>Algebra>Seeing Structure in Expressions>Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems.

Let

b_{i} > 1

for

i = 1, 2, \dots ., 101 .

Suppose

\log_{e} b_{1}, \log_{e} b_{2}, \dots . ., \log_{e} b_{101}

are in Arithmetic Progression (A.P.) with the common difference

\log_{e} 2 .

Suppose

a_{1}, a_{2}, \dots ., a_{101}

are in A.P. such that

a_{1} = b_{1}

and

a_{51} = b_{51} .

t = b_{1} + b_{2} + \dots + b_{51}

and

s = a_{1} + a_{2} + \dots + a_{51}

, then

HARD

Mathematics>Algebra>Seeing Structure in Expressions>Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems.

Let

x, y, z

be three non-negative integers such that

x + y + z = 10

. The maximum possible value of

x y z + x y + y z + z x

MEDIUM

Mathematics>Algebra>Seeing Structure in Expressions>Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems.

Three positive numbers form an increasing

G . P .

If the middle term in this

G . P .

is doubled, the new numbers are in

A . P .

Then the common ratio of the

G . P .

is :

MEDIUM

Mathematics>Algebra>Seeing Structure in Expressions>Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems.

{(10)}^{9} + 2 {(11)}^{1} {(10)}^{8} + 3 {(11)}^{2} {(10)}^{7} + ...... + 10 {(11)}^{9} = k {(10)}^{9},

then

k

is equal to :

MEDIUM

Mathematics>Algebra>Seeing Structure in Expressions>Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems.

Let

a, b

and

c

be the

7^{t h}, 11^{t h}

and

13^{t h}

terms respectively of a non-constant A.P. If these are also the three consecutive terms of a G.P., then

\frac{a}{c}

is equal to:

HARD

Mathematics>Algebra>Seeing Structure in Expressions>Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems.

The number of real solutions of the equation

\sin^{- 1} (\sum_{i = 1}^{\infty} x^{i + 1} - x \sum_{i = 1}^{\infty} {(\frac{x}{2})}^{i}) = \frac{π}{2} - \cos^{- 1} (\sum_{i = 1}^{\infty} {(- \frac{x}{2})}^{i} - \sum_{i = 1}^{\infty} {(- x)}^{i})

lying in the interval

(- \frac{1}{2}, \frac{1}{2})

is____.

(Here, the inverse trigonometric functions

\sin^{- 1} x & \cos^{- 1} x

assume values in

[- \frac{π}{2}, \frac{π}{2}] & [0, π]

respectively.)

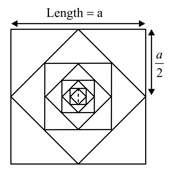
HARD

Mathematics>Algebra>Seeing Structure in Expressions>Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems.

Let $S_{1}$ be the sum of areas of the squares whose sides are parallel to coordinate axes. Let $S_{2}$ be the sum of areas of the slanted squares as shown in the figure. Then $S_{1} / S_{2}$ is

Question Image

MEDIUM

Mathematics>Algebra>Seeing Structure in Expressions>Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems.

a, b

and

c

be three distinct real numbers in G.P. and

a + b + c = x b,

then

x

cannot be:

HARD

Mathematics>Algebra>Seeing Structure in Expressions>Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems.

Let

f (x)

be a non-constant polynomial with real coefficients such that

f (\frac{1}{2}) = 100 & f (x) \leq 100

for all real

x .

Which of the following statements is NOT necessarily true?

MEDIUM

Mathematics>Algebra>Seeing Structure in Expressions>Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems.

The sum of the first

20

terms of the series

1 + \frac{3}{2} + \frac{7}{4} + \frac{15}{8} + \frac{31}{16} + \dots

MEDIUM

Mathematics>Algebra>Seeing Structure in Expressions>Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems.

Let

C_{0}

be a circle of radius

1

. For

n \geq 1,

let

C_{n}

be a circle whose area equals the area of a square inscribed in

C_{n - 1}

. Then

(\sum_{u = 0}^{\infty} area (C_{i}))

equals,

MEDIUM

Mathematics>Algebra>Seeing Structure in Expressions>Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems.

Let

z = 1 + a i

, be a complex number,

a > 0

, such that

z^{3}

is a real number. Then, the sum

1 + z + z^{2} + \dots . + z^{11}

is equal to :

MEDIUM

Mathematics>Algebra>Seeing Structure in Expressions>Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems.

If the

2^{n d}, 5^{t h}

and

9^{t h}

terms of a non-constant arithmetic progression are in geometric progression, then the common ratio of this geometric progression is

MEDIUM

Mathematics>Algebra>Seeing Structure in Expressions>Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems.

The sum of first

20

terms of the sequence

0.7, 0.77, 0.777, . . . . . .,

is :

HARD

Mathematics>Algebra>Seeing Structure in Expressions>Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems.

If $m$ is the $A . M .$ of two distinct real numbers $I$ and $n$ $(I, n > 1)$ and $G_{1}, G_{2} and G_{3}$ are three geometric means between $I and n$ , then $G_{1}^{4} + 2 G_{2}^{4} + G_{3}^{4}$ equals

MEDIUM

Mathematics>Algebra>Seeing Structure in Expressions>Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems.

The sum of the first

10

terms of the series

9 + 99 + 999 + . \dots .

The sum of an infinite geometric series is 162 and sum of its first n terms is 160. If the inverse of common ratio r is an integer, then which of the following options are correct?

Important Questions on Seeing Structure in Expressions

Learn and Prepare for any exam you want !

The sum of an infinite geometric series is $162$ and sum of its first $n$ terms is $160 .$ If the inverse of common ratio $r$ is an integer, then which of the following option $(s)$ are correct?