MEDIUM

Earn 100

The sum of an infinite geometric series is $2$ and the sum of geometric series made from the cube of this infinite series is $24 .$ Then the series is

78.16% studentsanswered this correctly

Important Questions on Sequences and Series

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progressions

Let

a, b

and

c

be in

G . P .

with common ratio

r,

where

a \neq 0

and

0 < r \leq \frac{1}{2} .

3 a, 7 b

and

15 c

are the first three terms of an

A . P .,

then the

4^{t h}

term of this

A . P .

is :

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progressions

Let

C_{0}

be a circle of radius

1

. For

n \geq 1,

let

C_{n}

be a circle whose area equals the area of a square inscribed in

C_{n - 1}

. Then

(\sum_{u = 0}^{\infty} area (C_{i}))

equals,

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progressions

If three distinct numbers

a, b, c

are in G.P. and the equations

a x^{2} + 2 b x + c = 0

and

d x^{2} + 2 e x + f = 0

have a common root, then which one of the following statements is correct?

EASY

Mathematics>Algebra>Sequences and Series>Geometric Progressions

The product of three consecutive terms of a

G . P .

512

. If

4

is added to each of the first and the second of these terms, the three terms now form an

A . P .

, then the sum of the original three terms of the given

G . P .

is :

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progressions

The sum of first

20

terms of the sequence

0.7, 0.77, 0.777, . . . . . .,

is :

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progressions

α, β

and

γ

are three consecutive terms of a non-constant G.P. Such that the equations

α x^{2} + 2 β x + γ = 0

and

x^{2} + x - 1 = 0

have a common root, then

α (β + γ)

is equal to:

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progressions

If the

2^{n d}, 5^{t h}

and

9^{t h}

terms of a non-constant arithmetic progression are in geometric progression, then the common ratio of this geometric progression is

EASY

Mathematics>Algebra>Sequences and Series>Geometric Progressions

The product

2^{\frac{1}{4}} \cdot 4^{\frac{1}{16}} \cdot 8^{\frac{1}{48}} \cdot 16^{\frac{1}{128}} \cdot . . . .

\infty

is equal to:

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progressions

The sum of the

3^{r d}

and the

4^{t h}

terms of a

G . P .

60

and the product of its first three terms is

1000.

If the first term of this

G . P .

is positive, then its

7^{t h}

term is:

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progressions

The quotient when

1 + x^{2} + x^{4} + . . . + x^{34}

is divided by

1 + x + x^{2} + . . . + x^{17}

HARD

Mathematics>Algebra>Sequences and Series>Geometric Progressions

Let

b_{i} > 1

for

i = 1, 2, \dots ., 101 .

Suppose

\log_{e} b_{1}, \log_{e} b_{2}, \dots . ., \log_{e} b_{101}

are in Arithmetic Progression (A.P.) with the common difference

\log_{e} 2 .

Suppose

a_{1}, a_{2}, \dots ., a_{101}

are in A.P. such that

a_{1} = b_{1}

and

a_{51} = b_{51} .

t = b_{1} + b_{2} + \dots + b_{51}

and

s = a_{1} + a_{2} + \dots + a_{51}

, then

HARD

Mathematics>Algebra>Sequences and Series>Geometric Progressions

If $m$ is the $A . M .$ of two distinct real numbers $I$ and $n$ $(I, n > 1)$ and $G_{1}, G_{2} and G_{3}$ are three geometric means between $I and n$ , then $G_{1}^{4} + 2 G_{2}^{4} + G_{3}^{4}$ equals

EASY

Mathematics>Algebra>Sequences and Series>Geometric Progressions

If the sum of an infinite GP be

9

and sum of first two terms be

5

then their common ratio is …..

EASY

Mathematics>Algebra>Sequences and Series>Geometric Progressions

Let

a_{1}, a_{2}, {\dots . . a}_{10}

be a G.P. If

\frac{a_{3}}{a_{1}} = 25,

then

\frac{a_{9}}{a_{5}}

equals:

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progressions

The greatest positive integer

k,

for which

49^{k} + 1

is a factor of the sum

49^{125} + 49^{124} + \dots + 49^{2} + 49 + 1,

HARD

Mathematics>Algebra>Sequences and Series>Geometric Progressions

Let

a_{n}

be the

n^{t h}

term of a G.P. of positive terms. If

\sum_{n = 1}^{100} a_{2 n + 1} = 200

and

\sum_{n = 1}^{100} a_{2 n} = 100,

then

\sum_{n = 1}^{200} a_{n}

is equal to:

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progressions

x = \sum_{n = 0}^{\infty} {(- 1)}^{n} \tan^{2 n} θ

and

y = \sum_{n = 0}^{\infty} \cos^{2 n} θ,

for

0 < θ < \frac{π}{4},

then:

HARD

Mathematics>Algebra>Sequences and Series>Geometric Progressions

Let $S_{1}$ be the sum of areas of the squares whose sides are parallel to coordinate axes. Let $S_{2}$ be the sum of areas of the slanted squares as shown in the figure. Then $S_{1} / S_{2}$ is

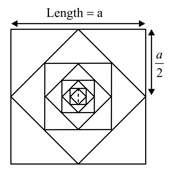
Question Image

HARD

Mathematics>Algebra>Sequences and Series>Geometric Progressions

The number of real solutions of the equation

\sin^{- 1} (\sum_{i = 1}^{\infty} x^{i + 1} - x \sum_{i = 1}^{\infty} {(\frac{x}{2})}^{i}) = \frac{π}{2} - \cos^{- 1} (\sum_{i = 1}^{\infty} {(- \frac{x}{2})}^{i} - \sum_{i = 1}^{\infty} {(- x)}^{i})

lying in the interval

(- \frac{1}{2}, \frac{1}{2})

is____.

(Here, the inverse trigonometric functions

\sin^{- 1} x & \cos^{- 1} x

assume values in

[- \frac{π}{2}, \frac{π}{2}] & [0, π]

respectively.)

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progressions

Let

a, b

and

c

be the

7^{t h}, 11^{t h}

and

13^{t h}

terms respectively of a non-constant A.P. If these are also the three consecutive terms of a G.P., then

\frac{a}{c}

is equal to:

The sum of an infinite geometric series is 2 and the sum of geometric series made from the cube of this infinite series is 24. Then the series is

Important Questions on Sequences and Series

Learn and Prepare for any exam you want !

The sum of an infinite geometric series is $2$ and the sum of geometric series made from the cube of this infinite series is $24 .$ Then the series is