The type of graph between length of a simple pendulum and time period is -
Important Questions on Oscillations
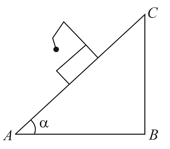
A simple pendulum is attached to a block which slides without friction down an inclined plane having an angle of inclination as shown while the block is sliding down the pendulum oscillates in such a way that at its mean position the direction of the string is,
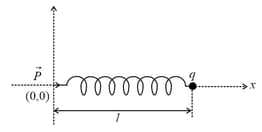
One end of a spring of negligible unstretched length and spring constant is fixed at the origin . A point particle of mass carrying a positive charge is attached at its other end. The entire system is kept on a smooth horizontal surface. When a point dipole pointing towards the charge is fixed at the origin, the spring gets stretched to a length and attains a new equilibrium position (see figure below). If the point mass is now displaced slightly by from its equilibrium position and released, it is found to oscillate at frequency The value of is _______.
[Consider the spring as massless]
A simple pendulum of length is made to oscillate with amplitude of degrees. The acceleration due to gravity is . Let The time period of oscillation of this pendulum will be
The position co-ordinates of a particle moving in a coordinate system is given by
and
The speed of the particle is:
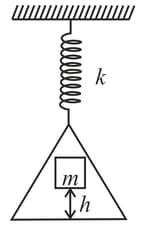
A load of mass falls from a height on the scale pan hung from a spring as shown. If the spring constant is and the mass of the scale pan is zero and the mass does not bounce relative to the pan, then the amplitude of vibration is
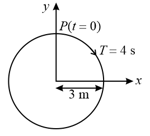
-projection of the radius vector of rotating particle is

