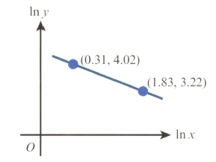
The variables and satisfy the equation , where and are constants. The graph of against is a straight line passing through the points and as shown in the diagram. Find the value of and the value of correct to significant figures.


Important Questions on Logarithmic and Exponential Functions
Convert from exponential form to logarithmic form.
Solve the equation, giving your answers correct to significant figures.
Variables and are related so that, when is plotted on the vertical axis and is plotted on the horizontal axis, a straight-line graph passing through the points and is obtained.
Express in terms of .
The mass, grams, of a radioactive substance is given by the formula , where is the time in days after the mass was first recorded and and are constants.
The table below shows experimental values of and .
Draw the graph of against .
The temperature, , of a hot drink, minutes after it is made, can be modelled by the equation , where and are constants. The table below shows experimental values of and .
Estimate:
the time taken for the temperature to reach
The polynomial is defined by .
Show that and factorise completely.
The polynomial is defined by .
Given that , state the value of and hence find correct to significant figures.
