MEDIUM

Earn 100

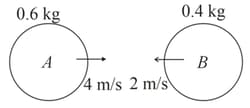
The velocities of two steel balls before impact are shown. If after head-on impact the velocity of ball $B$ is observed to be $3 m s^{- 1}$ to the right, the coefficient of restitution is

50% studentsanswered this correctly

Important Questions on Centre of Mass, Momentum and Collisions

HARD

Physics>Mechanics>Centre of Mass, Momentum and Collisions>Elastic and Inelastic Collisions

An alpha- particle of mass

m

suffers

1 -

dimensional elastic collision with a nucleus at rest of unknown mass. It is scattered directly backwards losing

64 %

of its initial kinetic energy. The mass of the nucleus is

MEDIUM

Physics>Mechanics>Centre of Mass, Momentum and Collisions>Elastic and Inelastic Collisions

A satellite of mass

M

is in a circular orbit of radius

R

about the center of the earth. A meteorite of the same mass, falling towards the earth, collides with the satellite completely inelastic. The speeds of the satellite and the meteorite are the same, just before the collision. The subsequent motion of the combined body will be:

HARD

Physics>Mechanics>Centre of Mass, Momentum and Collisions>Elastic and Inelastic Collisions

An object is dropped from a height

h

from the ground. Every time it hits the ground it loses

50 %

of its kinetic energy. The total distance covered as

t \to \infty

is:

HARD

Physics>Mechanics>Centre of Mass, Momentum and Collisions>Elastic and Inelastic Collisions

In a collinear collision, a particle with an initial speed

v_{0}

strikes a stationary particle of the same mass. If the final total kinetic energy is

50 %

greater than the original kinetic energy, the magnitude of the relative velocity between the two particles, after the collision, is

HARD

Physics>Mechanics>Centre of Mass, Momentum and Collisions>Elastic and Inelastic Collisions

A block of mass $m = 10 kg$ rests on a horizontal table. The coefficient of friction between the block and the table is $0.05$ . When hit by a bullet of mass $50 g$ moving with speed $v$ , that gets embedded in it, the block moves and comes to stop after moving a distance of $2 m$ on the table. If a freely falling object were to acquire speed $\frac{v}{10}$ after being dropped from height $H$ , then neglecting energy losses and taking $g = 10 m s^{- 2}$ , the value of $H$ is close to

HARD

Physics>Mechanics>Centre of Mass, Momentum and Collisions>Elastic and Inelastic Collisions

It is found that if a neutron suffers an elastic collinear collision with a deuterium at rest, the fractional loss of its energy is

P_{d}

, while for its similar collision with a carbon nucleus at rest, the fractional loss of energy is

P_{c}

. The values of

P_{d}

and

P_{c}

are respectively

HARD

Physics>Mechanics>Centre of Mass, Momentum and Collisions>Elastic and Inelastic Collisions

A simple pendulum, made of a string of length

l

and

a

bob of mass

m,

is released from a small angle

θ_{0} .

It strikes a block of mass

M,

kept on horizontal surface at its lowest point of oscillations, elastically. It bounces back and goes up to an angle

θ_{1} .

Then

M

is given by:

EASY

Physics>Mechanics>Centre of Mass, Momentum and Collisions>Elastic and Inelastic Collisions

A body of mass

m_{1}

moving with an unknown velocity of

v_{1} \hat{i},

undergoes a collinear collision with a body of mass

m_{2}

moving with a velocity

v_{2} \hat{i} .

After the collision,

m_{1}

and

m_{2}

move with velocities of

v_{3} \hat{i}

and

v_{4} \hat{i},

respectively. If

m_{2} = 0.5 m_{1}

and

v_{3} = 0.5 v_{1},

then

v_{1}

is:

HARD

Physics>Mechanics>Centre of Mass, Momentum and Collisions>Elastic and Inelastic Collisions

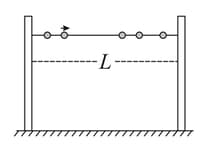
A large number $(n)$ of identical beads, each of mass $m$ and radius $r$ are strung on a thin smooth rigid horizontal rod of length $L (L ≫ r)$ and are at rest at random positions. The rod is mounted between two rigid supports (see figure). If one of the beads is now given a speed $v$ , the average force experienced by each support after a long time is (assume all collisions are elastic):
Question Image

HARD

Physics>Mechanics>Centre of Mass, Momentum and Collisions>Elastic and Inelastic Collisions

An oscillator of mass

M

is at rest in its equilibrium position in a potential,

V = \frac{1}{2} k {(x - X)}^{2}

. A particle of mass

m

comes from the right with speed

u

and collides completely inelastic with

M

and sticks to it. This process repeats every time the oscillator crosses its equilibrium position. The amplitude of oscillations after

13

collisions is:

(M = 10, m = 5, u = 1, k = 1)

EASY

Physics>Mechanics>Centre of Mass, Momentum and Collisions>Elastic and Inelastic Collisions

On a frictionless surfaces, a block of mass

M

moving at speed

v

collides elastically with another block of same mass

M

which is initially at rest. After collision the first block moves at an angle

θ

to its initial direction and has a speed

\frac{v}{3}

. The second block's speed after the collision is:

MEDIUM

Physics>Mechanics>Centre of Mass, Momentum and Collisions>Elastic and Inelastic Collisions

A particle of mass

m

moving in the

x

direction with speed

2 v

is hit by another particle of mass

2 m

moving in the

y

direction with speed

v .

If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to:

HARD

Physics>Mechanics>Centre of Mass, Momentum and Collisions>Elastic and Inelastic Collisions

A body

A

of mass

m = 0.1 k g

has an initial velocity of

3 \hat{i} m s^{- 1}

. It collides elastically with another body

B

of the same mass which has an initial velocity of

5 \hat{j} m s^{- 1}

. After the collision,

A

moves with a velocity

\vec{v} = 4 (\hat{i} + \hat{j}) m s^{- 1}

. The energy of

B

after the collision is written as

\frac{x}{10} J

. The value of

x

HARD

Physics>Mechanics>Centre of Mass, Momentum and Collisions>Elastic and Inelastic Collisions

Two particles

A

and

B

of equal mass

M

are moving with the same speed

v

as shown in figure. They collide completely inelastic and move as a single particle

C

. The angle

θ

that the path of

C

makes with the

X

-axis is given by-

Question Image

MEDIUM

Physics>Mechanics>Centre of Mass, Momentum and Collisions>Elastic and Inelastic Collisions

Body

A

of mass

4 m

moving with speed

u

collides with another body

B

of mass

2 m

at rest. The collision is head on and elastic in nature. After the collision, the fraction of energy lost by the colliding body

A

MEDIUM

Physics>Mechanics>Centre of Mass, Momentum and Collisions>Elastic and Inelastic Collisions

A particle of mass

m

is moving with speed

2 v

and collides with a mass

2 m

moving with speed

v

in the same direction. After the collision, the first mass is stopped completely while the second one splits into two particles each of mass

m,

which move at an angle

45^{o}

with respect to the original direction. The speed of each of the moving particle will be

MEDIUM

Physics>Mechanics>Centre of Mass, Momentum and Collisions>Elastic and Inelastic Collisions

A body of mass

2 k g

makes an elastic collision with a second body at rest and continues to move in the original direction but with one fourth of its original speed. What is the mass of the second body?

EASY

Physics>Mechanics>Centre of Mass, Momentum and Collisions>Elastic and Inelastic Collisions

Two identical balls

A

and

B

having velocities of

0.5 m s^{- 1}

and

- 0.3 m s^{- 1}

, respectively, collide elastically in one dimension. The velocities of

B

and

A

after the collision, respectively, will be

MEDIUM

Physics>Mechanics>Centre of Mass, Momentum and Collisions>Elastic and Inelastic Collisions

This question has $Statement - I$ and $Statement - II$ of the four choices given after the Statements, choose the one that best describes the two Statements.

$Statement - I:$ A point particle of mass $m$ moving with speed $ν$ collides with stationary point particle of mass $M$ . If the maximum energy loss possible is given as
$f (\frac{1}{2} m ν^{2})$ then $f = (\frac{m}{M + m})$ .

$Statement - II:$ Maximum energy loss occurs when the particles get stuck together as a result of the collision.

EASY

Physics>Mechanics>Centre of Mass, Momentum and Collisions>Elastic and Inelastic Collisions

A ball is thrown vertically downwards from a height of

20 m

with an initial velocity

v_{0}

. It collides with the ground, loses

50

percent of its energy in collision and rebounds to the same height. The initial velocity

v_{0}

is: (Take

g = 10 m s^{- 2}

)

The velocities of two steel balls before impact are shown. If after head-on impact the velocity of ball B is observed to be 3 m s-1 to the right, the coefficient of restitution is

Important Questions on Centre of Mass, Momentum and Collisions

Learn and Prepare for any exam you want !

The velocities of two steel balls before impact are shown. If after head-on impact the velocity of ball $B$ is observed to be $3 m s^{- 1}$ to the right, the coefficient of restitution is