The velocity of a particle moving in the positive direction of the $x$-axis varies as $v=\alpha \sqrt{x}$ where $\alpha$ is a positive constant. Assuming that at the moment $t=0$ the particle was located at the point $x=0$, find:

$\left(\mathrm{a}\right)$ The time dependence of the velocity and the acceleration of the particle.

$\left(\mathrm{b}\right)$ The mean velocity of the particle averaged over the time that the particle takes to cover the first $s \mathrm{metres}$ of the path.

When a model rocket is launched, the propellant burns for a few seconds, accelerating the rocket upward. After burnout, the rocket moves upward for a while and then begins to fall. A parachute opens shortly after the rocket starts down. The parachute slows the rocket to keep it from breaking when it lands. The figure here shows velocity data from the flight of the model rocket. Use the data to answer the following.

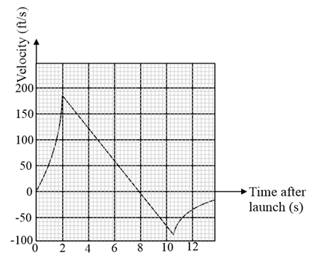
$\left(\mathrm{a}\right)$ How fast was the rocket climbing when the engine stopped? 

$\left(\mathrm{b}\right)$ For how many seconds did the engine burn?

$\left(\mathrm{c}\right)$ When did the rocket reach its highest point? What was its velocity then?

$\left(\mathrm{d}\right)$ When did the parachute open up? How fast was the rocket falling then?

$\left(\mathrm{e}\right)$ How long did the rocket fall before the parachute opened?

$\left(\mathrm{f}\right)$ When was the rocket's acceleration greatest?

$\left(\mathrm{g}\right)$ When was the acceleration constant? What was its value then (to the nearest integer)?

A particle of mass ${10}^{-2} \mathrm{kg}$ is moving along the $x$-axis under the influence of a force $F\left(x\right)=-\frac{K}{2x^2}$, where $K={10}^{-2} \mathrm{N} {\mathrm{m}}^2$. At the time $t=0$ it is at $x=1.0 \mathrm{m}$ and its velocity is $v=0$. Find:

$\left(\mathrm{a}\right)$ Its velocity when it reaches $x=0.50 \mathrm{m}$.

$\left(\mathrm{b}\right)$ The time at which it reaches $x=0.25 \mathrm{m}$.

Two particles are thrown from the top of a tower with the same speed in upward and downward directions simultaneously. If the first particle hits the ground in time $t$ and the second particle takes time $t_0$ after the first one hitting the ground to hit the ground. Then find

$\left(\mathrm{a}\right)$ Maximum height attained by the second particle above the tower.

$\left(\mathrm{b}\right)$ Height of tower 

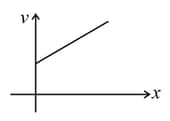
A particle moves along $x$-axis in a positive direction. Its acceleration $a$ is given as $a=cx+d$, where $x$ denotes the $x$-coordinate of particle, $c$ and $d$ are positive constants. For velocity-position graph of particle to be of type as shown in figure, find the value of speed (in $\mathrm{m} {\mathrm{s}}^{-1}$) of particle at $x=0$. Take $c=1 {\mathrm{s}}^{-2}$ and $d=3 \mathrm{m} {\mathrm{s}}^{-2}$