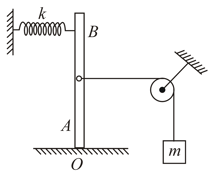
To determine the MI of an object, we can use torsional pendulum method. If the torsional constant of the apparatus (a disc suspended by the thread) is $C=16 \mathrm{Nm} {\mathrm{rad}}^{-1}.$ If the empty torsional pendulum (without the man) has a time period $T_0=2 \mathrm{s}$ and that with the man is $T=2.5 \mathrm{s},$ find the MI of the man. (Take ${\pi }^2=10$)

A uniform disc of mass $m$ and radius $R$ is connected with two light springs $1$ and $2.$ The springs are connected at the highest point $M$ and the $\mathrm{CM} \text{'}\mathrm{N}\text{'}$ of the disc. The other ends of the springs are rigidly attached with vertical walls. If we shift the CM in horizontal by a small distance, the disc oscillates simple harmonically. Assuming a perfect rolling of the disc on the horizontal surface, find the angular frequency of oscillation.

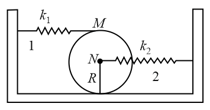
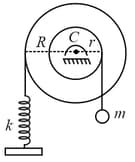
A stepped pulley having mass $m,$ radius $R$ and radius of gyration $k$ is connected with two ideal springs of stiffness $k$ and $k_2$ as shown in the figure. If the pulley rolls without sliding, find the angular frequency of its oscillation.

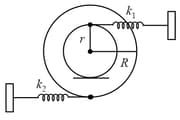
A stepped disc of mass $M$ and radius $R$ is pivoted at its center $C$ smoothly. An inextensible string connected with a light spring of stiffness $k$ passes over the pulley. One end of the string is rigidly connected with the ground and the other end is attached to a body of mass $m.$ If the string does not slide on the pulley, find the angular frequency of oscillation of the system.

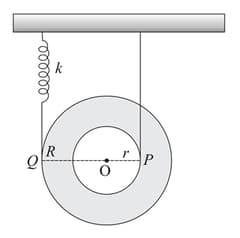
A disc of mass $m$ hanged by a string is attached at $P$ and a spring of stiffness $k$ is attached at $O.$ Find the frequency of small angular oscillation of the disc if the string does not slide over the pulley. Assume $I_0=MI$ of the disc about $O.$

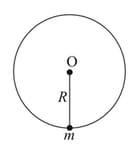
A disc of mass $M=2 \mathrm{m}$ and radius $R$ is pivoted at its centre. The disc is free to rotate in the vertical plane about its horizontal axis through its centre $O.$ A particle of mass $m$ is stuck on the periphery of the disc. Find the frequency of small oscillations of the system about its equilibrium position.

A square plate of mass $M$ and side length $L$ is hinged at one of its vertex $\left(A\right)$ and is free to rotate about it. Find the time period of small oscillations if

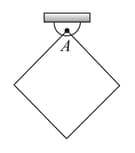
The plate performs oscillations in the verticai plane of the figure. (Axis is perpendicular to figure.)

A square plate of mass $M$ and side length $L$ is hinged at one of its vertex $\left(A\right)$ and is free to rotate about it. Find the time period of small oscillations if

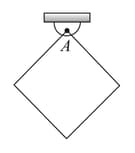
The plate performs oscillations about a horizontal axis passing through $A$ lying in the plane of the figure.