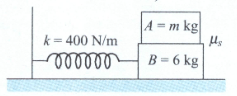
Two blocks lie on each other and are connected to a spring as shown in the figure. What should be the mass of block $A$ placed on block $B$ of mass $6\mathrm{kg}$ so that the system is period is $1\mathrm{s}$. Assuming no slipping, what should be the minimum value of coefficient of static friction $\mu$, for which block $A$ will not slip relative to block $B$, if block $B$ is displaced $50\mathrm{mm}$ from equilibrium position and released?

(Given: $g=10{\mathrm{ms}}^{-2}$ and ${\pi }^2=10$)

 

The potential energy $\left(U\right)$ of a body of unit mass moving in a one-dimensional conservative force field is given by $U=\left(x^2-4x+3\right)$. All units are in SI unit. Find the equilibrium position of the body.

The potential energy $\left(U\right)$ of a body of unit mass moving in a one-dimensional conservative force field is given by $U=\left(x^2-4x+3\right)$. $U$ and $x$ are in SI units. Show that oscillations of the body about this equilibrium position are in simple harmonic motion and find its time period.

The potential energy $\left(U\right)$ of a body of unit mass moving in a one-dimensional conservative force field is given by $U=\left(x^2-4x+3\right)$. All units are in SI. Find the amplitude of oscillations if the speed of the body at equilibrium position is $2\sqrt{6} \mathrm{m} {\mathrm{s}}^{-1}$. 

In the figure shown, the block $A$ of mass $M$ collides with the identical block $B$ and after collision they stick together. Calculate the amplitude of resultant vibration.

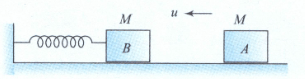
Figure shows a block $P$ of mass $m$ resting on a horizontal smooth floor at a distance $l$ from a rigid wall. Block is pushed towards right by a distance $\frac{3l}{2}$ and released. When block passes from its mean position another block of mass $m_1$ is placed on it which sticks to it due to friction. Find the value of $m_1$ so that the combined block just collides with the left wall.

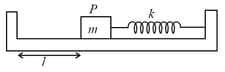
Figure shows a block of mass $m$ resting on a smooth horizontal ground attached to one end of a spring of force constant $k$ in natural length. If another block of same mass and moving with a velocity $u$ towards right is placed on the block which stick to it due to friction, find the time it will take to reach its extreme position. Also find the amplitude of oscillations of the combined mass $2 \mathrm{m}.$

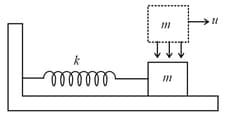
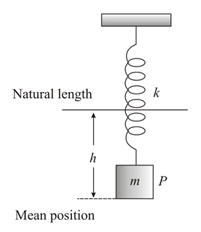
Figure shows a spring block system hanging in equilibrium. If a velocity $v_0$ is imparted to the block in downward direction, find the amplitude of SHM of the block and the time after which it will reach a point at half of the amplitude of block.