Two bodies of masses, $m=0.30 \mathrm{kg}$ and $2m$, are connected by a long string of negligible mass. The string is looped over a pulley and, with the string taut, the bodies are released at time $t=0$ so that the heavier one descends and the lighter one ascends. At time $t=4.0 \mathrm{s}$, the lighter one undergoes a fully inelastic collision with a third body of mass $m$. Because the first two bodies move in rigid fashion, the collision is effectively between the third body and the system of the first two bodies.
(a) Just after the collision, what is the speed of the three bodies?
(b) By how much was the kinetic energy of the descending body decreased because of the collision?

Two titanium spheres approach each other head-on with the same speed and collide elastically. After the collision, one of the spheres, whose mass is $250 \mathrm{g}$, remains at rest.

(a) What is the mass of the other sphere?

(b) What is the speed center of mass of the two sphere if the initial speed of each sphere is $2.00 \mathrm{m} {\mathrm{s}}^{-1}?$

Block $1$ of mass $m_1$ slides along a frictionless floor and into a one-dimensional elastic collision with stationary block $2$ of mass $m_2=3m_1$. Prior to the collision, the centre of mass of the two blocks system had a speed of $3.00 \mathrm{m} {\mathrm{s}}^{-1}$. Afterward, what are the speeds of (a) the centre of mass and (b) block $2$?

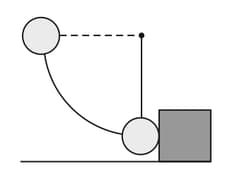
A steel ball of mass $0.600 \mathrm{kg}$ is fastened to a cord that is $70.0 \mathrm{cm}$ long and fixed at the far end. The ball is then released when the cord is horizontal In figure shows below At the bottom of its path, the ball strikes a $2.80 \mathrm{kg}$ steel block initially at rest on a frictionless surface. The collision is elastic. Find (a) the speed of the ball and (b) the speed of the block, both just after the collision.

Block$1$ , with mass $m_1$ and speed $3.0 \mathrm{m} {\mathrm{s}}^{-1}$ slides along an $x$ axis on a frictionless floor and then undergoes a one-dimensional elastic collision with stationary block $2$, with mass $m_2=0.40m_1$. The two blocks then slide into a region where the coefficient of kinetic friction is $0.50$, there they stop. How far into that region do (a) block$1$ and (b) block $2$ slide?

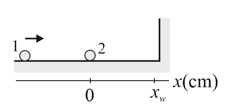
In figure shown below particle $1$ of mass $m_1=0.30 \mathrm{kg}$ slides rightward along an $x$  axis on a frictionless floor with a speed of  $2.0 \mathrm{m} {\mathrm{s}}^{-1}$. When it reaches $x=0$, it undergoes a one-dimensional elastic collision with stationary particle $2$ of mass $m_2=0.40 \mathrm{kg}$. Particle $2$ then reaches a wall at $x_w=70 \mathrm{cm}$, it bounces from the wall with no loss of speed. At what position on the $x$ axis does particle $2$ then collide with particle $1$?

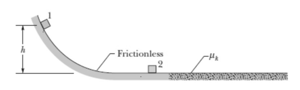
In figure shown below block $1$ of mass $m_1$ slides from rest along a frictionless ramp from height $h=3.00 \mathrm{m}$ and then collides with stationary block $2$, which has mass $m_2=2.00 {\mathrm{m}}_1.$ After the collision, block $2$ slides into a region where the coefficient of kinetic friction ${\mu }_2$ is $0.450$ and comes to a stop in distance $d$ within that region. What is the value of distance $d$ if the collision is (a) elastic and (b) completely inelastic?

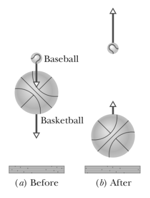
 A small ball of mass $m$ is aligned above a larger ball of mass $M=0.63 \mathrm{kg}$ (with a slight separation, as with the baseball and basketball in figure shown below), and the two are dropped simultaneously from a height of $h=1.8 \mathrm{m}$. (Assume the radius of each ball is negligible relative to $h$) (a) If the larger ball rebounds elastically from the floor and then the small ball rebounds elastically from the larger ball, what value of $m$ results in the larger ball stopping when it collides with the small ball?
(b) What height does the small ball then reach in the figure shown below: [ take $g=10 m/s^2$]