Two particle performs simple harmonic motion with time period of second andsecond respectively. At both were in their mean position and moving in the same direction. After what minimum non zero time they will be in phase again.
Important Questions on Simple Harmonic Motion
A simple pendulum suspended from the ceiling of a stationary lift has a time period . When the lift descends at uniform speed, the time period is . When the lift descends with constant acceleration, the time period is . Which of the following is correct?
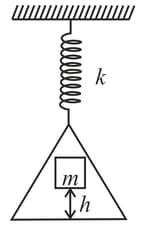
A load of mass falls from a height on the scale pan hung from a spring as shown. If the spring constant is and the mass of the scale pan is zero and the mass does not bounce relative to the pan, then the amplitude of vibration is
An ideal gas enclosed in a vertical cylindrical container supports a freely moving piston of mass . The piston and the cylinder have equal cross-sectional area . When the piston is in equilibrium, the volume of the gas is and its pressure is . The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
[Assume the system is in space.]
Match List (Event) with List (Order of the time interval for the happening of the event) and select the correct option from the options given below the lists.
| List-I | List-II | ||
|---|---|---|---|
| The rotation period of earth | |||
| Revolution period of earth | |||
| Period of a light wave | |||
| Period of a sound wave |

