We arrange for two blocks to undergo simple harmonic motion along adjacent, parallel paths with amplitude $A$. What is their phase difference if they pass each other in the opposite direction whenever their displacement is $\frac{A}{2}$?

An oscillating block-spring system has mechanical energy of $2.00 \mathrm{J}$, an amplitude of $10.0 \mathrm{cm}$, and a maximum speed of $0.800 \mathrm{m} {\mathrm{s}}^{-1}$. Find

(a) the spring constant,

(b) the mass of the block and 

(c) the frequency of oscillation.

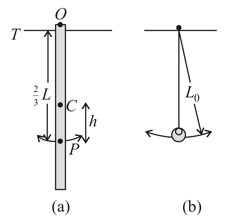
In the figure, a meter stick swings about a pivot point at one end, at distance $h$ from the stick’s centre of mass. (a) What is the period of oscillation $T$? (b) What is the distance $L_0$ between the pivot point $\mathrm{O}$ of the stick and the centre of oscillation of the stick? (c) If the physical pendulum of the figure $\mathrm{a}$ and the associated sample problem is inverted and suspended at point $\mathrm{P}$, what is its period of oscillation? (d) Is the period now greater than, less than, or equal to its previous value? [Take $g=9.8 \mathrm{m} {\mathrm{s}}^{-2}$]

An automobile can be considered to be mounted on four identical spring as far as vertical oscillation are concerned. The springs of a certain car are adjusted so that the oscillations have a frequency of $3.00 \mathrm{Hz}$.

(a) What is the spring constant of each spring if the mass of the car is $2110 \mathrm{kg}$ and the mass is evenly distributed over the spring?

(b) What will be the oscillation frequency if five passenger averaging $85.0 \mathrm{kg}$ each ride in the car with an even distribution of mass?

The position function $x=(6.0 \mathrm{m})\cos \left(\left[( 3\pi \mathrm{rad} {\mathrm{s}}^{-1})\mathrm{t} +\frac{\pi }{3} \mathrm{rad}\right]\right)$ gives the simple harmonic motion of a body. At $t=2.1 \mathrm{s}$.

What are the

(a) displacement,

(b) velocity,

(c) acceleration, and 

(d) phase of the motion?

Also, what are the

(e) frequency and

(f) period of the motion ?

Two particles oscillate in simple harmonic motion along a common straight-line segment of length $A$. Each particle has a period of $1.5 \mathrm{s}$, but they differ in phase by $\frac{\pi }{6} \mathrm{rad}$.

(a) How far apart are they (in terms of $A$) $0.60 \mathrm{s}$, after the lagging particle leaves one end of the path?

(b) Are they then moving in the same direction, towards each other, or away from each other?

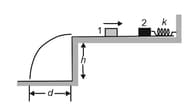
A block $1$ of mass $0.200 \mathrm{kg}$ sliding to the right over a frictionless elevated surface at a speed of $10.0 \mathrm{m} {\mathrm{s}}^{-1}$. The block undergoes an elastic collision with stationary block $2$, which is attached to a spring of spring constant $1208.5 \mathrm{N} {\mathrm{m}}^{-1}$.(Assume that the spring does not affect the collision.) After the collision, block $2$ oscillates in SHM with a period of $0.140 \mathrm{s}$, and block $1$ slides off the opposite end of the elevated surface, landing a distance $d$ from the base of that surface after falling height $h=6.20 \mathrm{m}$. What is the value of $d$ ?