What are the crystallographic parameter of hexagonal, monoclinic and triclinic unit cell respectively.

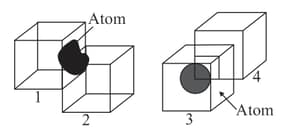
Following diagrams show identical-cubes such that edge of cube? lies exactly in the middle of one of the faces of Cube$1$ and Cube $4$ has a corner at the body center of the Cube$3$. Find the contributions(in fraction) of the spheres shown to each of the cubes.

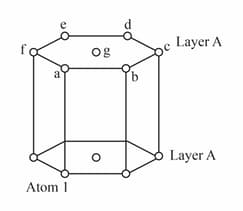
Consider a corner atom of ${\mathrm{I}}^{\mathrm{st}}$ layer of an $\mathrm{HCP}$ unit cell showing alternate $\mathrm{AA}$ layer. Find
(i) Find identical atoms ($\text{III}$ layer) with respect to the distances from the atom $1$.
(ii) Arrange the distances in ascending order.

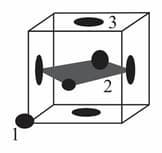
Following figure shows an $\mathrm{FCC}$ unit cell with atoms of radius $\mathrm{r}$ marked ($1$corner ), $2$(face center), $3$(face center). A quadrilateral is also shown by joining the centers of $4$ face centered atoms. Find:
(i) The distances between atoms $1\& 2, 2 \& 3$ and $1 \& 3$.
(ii) The shape and dimensions of the quadrilateral.