EASY
Earn 100
With usual notations, if in , is semi-perimeter and , then is
(a)an obtuse angle triangle
(b)an equilateral triangle
(c)a right angled triangle
(d)an acute angle triangle
20% studentsanswered this correctly
Important Questions on Trigonometric Functions
HARD
Let and be positive real numbers. Suppose and are the lengths of the sides of a triangle opposite to its angles and respectively. If , then which of the following statements is/are TRUE?
MEDIUM
Consider four triangles having sides and . Among these the triangle having maximum area has sides
MEDIUM
In a , points and are on and , respectively, such that is parallel to . Which of the two following equalities always hold? (Here, denotes the area of ).
.
.
HARD
Let be a triangle such that and . Choose points on respectively, such that . Then is
HARD
Let be a square and let be point on segment such that . Let be a point on segment such that . Then the ratio of the area of quadrilateral to the area of the square is
MEDIUM
With usual notations, in , if , then
HARD
In the figure given below, if the areas of the two regions are equal then which of the following is true?
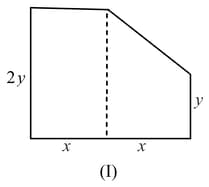
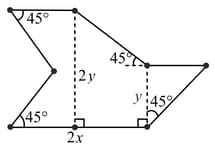
MEDIUM
Let be a convex cyclic quadrilateral. Suppose is a point in the plane of the quadrilateral such that sum of its distances from the vertices of is the least. If , what is the maximum possible area of
EASY
If the sides of triangle are and Then the area (in sq cm) of triangle is
HARD
Suppose we have two circles of radius each in the plane such that the distance between their centres is . The area of the region common to both circles lies between
MEDIUM
In the lengths of sides and are and respectively. If the area of is and and are respectively the radii of circumcircle and incircle of , then the value of is equal to ______ .
HARD
In the figure given below, is a regular hexagon of side length unit, and are squares. Then the ratio equals
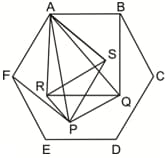
HARD
In a quadrilateral it is given that If is the radius of the circle inscribable in the quadrilateral, then what is the integer closest to
HARD
If and are lengths of two medians of a triangle, what is the maximum possible area of the triangle to the nearest integer?
MEDIUM
If are the sides of a and exradii are respectively then
MEDIUM
In a if and then the area of the triangle is
MEDIUM
Let be respectively the areas of a regular pentagon, regular hexagon and regular heptagon which are inscribed in a circle of radius . Then
HARD
In a rectangle points and are the mid-points of and respectively. Lines and when extended intersect at and lines and when extended intersect at . If the area of rectangle is square units, then the area of (in square units) is

