Write whether the following statements are True or False? Justify your answer:
Attempts to prove Euclid's fifth postulate using the other postulates and axioms led to the discovery of several other geometries.

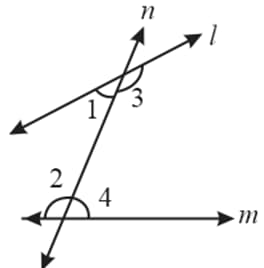
In the adjacent figure,  a line$n$ falls on lines$l$ and $m$ such that the sum of the interior angle$\angle 1$ and $\angle 2$ is less than $180°$.On which side of the transversal $n$ will the line $l$ and line $m$ meet?

In how many points two distinct lines can intersect?

Two distinct lines cannot have more than one point in common.

Does Euclid fifth postulate imply the existence of parallel lines? Explain.

How many books are there in Euclid’s Elements ?

In the following figure, name two pairs of non-intersecting line segments.

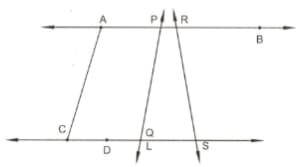
In the adjoining figure, name :

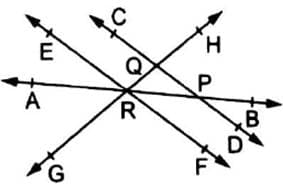
Two pairs of intersecting lines and their corresponding points of Intersection.

Is the following statement a direct consequence of Euclid's fifth postulate?
"There exists a pair of straight lines that are everywhere equidistant from one another."

Hint: Use play fairs axiom, which is equivalent to Euclid's fifth postulate.

Attempts to prove Euclid's fifth postulate using the other postulate and axioms led to the discovery of several other geometries.

If the diagonal of a square is ‘a’ units, what is the diagonal of the square, whose area is double that of the first square?