Binomial Theorem for Positive Integral Indices

The first five numbers are written in the third slanting row of the Pascal's Triangle. Then the squares of the triangular numbers are the sum of cubes of natural numbers. Write answer as$(\mathrm{Yes}/ \mathrm{No})$.

Check whether the following hexagonal shapes form a part of the Pascal's Triangle. Write the answer (Yes/ No).

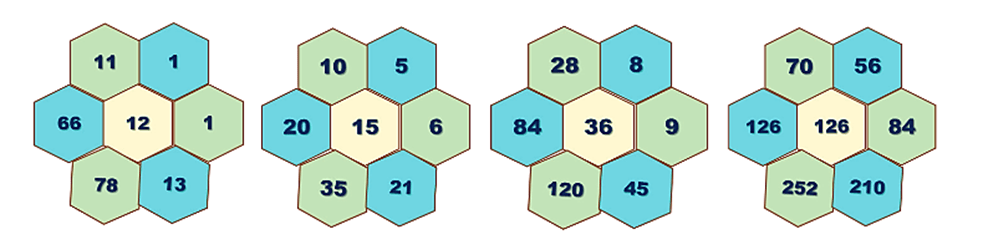
The sum of all the numbers in each row of Pascal’s Triangle is of the form $3^n$.

$\frac{1}{9!}+\frac{1}{3!7!}+\frac{1}{5!5!}+\frac{1}{7!3!}+\frac{1}{9!}$ is equal to

$\left({}_{ }{}^7{C}_0+{}^7{C}_1\right)+\left({}^7{C}_2+{}^7{C}_3\right)+\dots +\left({}^7{C}_6+{}^7{C}_7\right)=$

The sum to infinite terms of the series :

$\frac{7}{5}\left(1+\frac{1}{{10}^2}+\frac{1.3}{1.2}·\frac{1}{{10}^4}+\frac{1.3.5}{1.2.3}·\frac{1}{{10}^6}+\dots \dots .\infty \right)=$

Using binomial theorem, find the value of $(10.1{)}^6$.

${}^{25}C_4+\sum _{r=0}^4{}^{\left(29-r\right)}C_3=$

Find the value of ${}^{10}C_5+2·{}^{10}C_4+{}^{10}C_3$.

If $x=\frac{1}{5}+\frac{1.3}{5.10}+\frac{1.3.5}{5.10.15}+\dots ...\infty$ then $3x^2+6x=$

Find the number of terms in the expansion of $(2x+3y+z{)}^7$.

If $t=\frac{4}{5}+\frac{4\times 6}{5\times 10}+\frac{{\displaystyle 4\times 6\times 8}}{{\displaystyle 5\times 10\times 15}}+.................\infty$, then $9t=$

if n is positive integer and $x$ is any non zero real number, then $c_0+c_1\frac{x}{2}+c_2\frac{x^2}{3}+c_3\frac{x^3}{4}+.............+c_n\frac{x^n}{n+1}=$

In the expansion of ${\left(a+1+\frac{1}{a}\right)}^n$, where $n\in N$ there are $2029$ terms. Then $n=$

Using binomial theorem evaluate ${\left(0.99\right)}^5+{\left(1.01\right)}^5$(write the exact answer till the last decimal place).

If $a+b=1,$ then write the value of $\sum _{r=0}^n{}^{n}C_r{a}^r{b}^{n-r}$.

How many terms (only numerical value) are there in the expansion of ${\left[{\left(3x+y^2\right)}^9\right]}^4$.

Write the number of terms (only numerical value) in the expansion of ${\left(x^2+y\right)}^{30}$.

Find $\mathrm{n}$ in the binomial ${\left(\sqrt[3]{2}+\frac{1}{\sqrt[3]{3}}\right)}^n$ if the ratio of $7^{\mathrm{th}}$ term from the beginning to the$7^{\mathrm{th}}$ term from the end is $1/6$.

Find the coefficient of ${\mathrm{x}}^4$ in the expansion of ${\left(1+\mathrm{x}+{\mathrm{x}}^2+{\mathrm{x}}^3\right)}^{11}$.