Bernoulli Trials and Binomial Distribution

In binomial probability distribution, mean is $3$ and standard deviation is $\frac{3}{2}$. Then find the value of $p$.

The survey is conducted in a large factory. If $27\%$ of the factory workers weigh less than $65$ kg and that $25\%$ of the factory workers weigh more than $96$ kg.  [ use the standard values $P(Z<-0.6128\dots )=0.27\text{ and }P(Z<0.6744\dots )=0.75$]

Then the assumed weights of the factory workers is modelled by a normal distribution with mean $\mu$ and standard deviation $\sigma$.

Determine two simultaneous linear equations satisfied by $\mu$ and $\sigma$.

Find the values of $\mu$ and $\sigma$.

Find the expectation of number of heads in $30$ tosses of a fair coin.

Xsquared Potato Crisps runs a promotion for a week. In $0.01\%$ of the hundreds of thousands of bags produced there are gold tickets for a round-the-world trip. Let $B$ represent the number of bags of crisps opened until a gold ticket is found.

Hence show that the probability distribution function of $B$ is $f\left(b\right)=P\left(B=b\right)=0.0001{\left(0.9999\right)}^{b-1}$.

Determined to win a ticket, Yimo buys $10$ bags of crisps. Find the probability that she finds a gold ticket after opening no more than $10$ bags.

Xsquared Potato Crisps runs a promotion for a week. In $0.01\%$ of the hundreds of thousands of bags produced there are gold tickets for a round-the-world trip. Let $B$ represent the number of bags of crisps opened until a gold ticket is found.

Hence show that the probability distribution function of $B$ is $f\left(b\right)=P\left(B=b\right)=0.0001{\left(0.9999\right)}^{b-1}$.

State the domain of $f\left(b\right)$.

Xsquared Potato Crisps runs a promotion for a week. In $0.01\%$ of the hundreds of thousands of bags produced there are gold tickets for a round-the-world trip. Let $B$ represent the number of bags of crisps opened until a gold ticket is found.

Hence show that the probability distribution function of $B$ is $f\left(b\right)=P\left(B=b\right)=0.0001{\left(0.9999\right)}^{b-1}$.

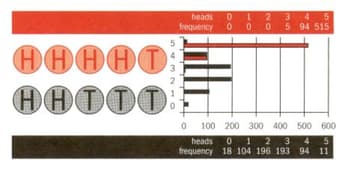
Zeke explores his biased coin in more detail. He design a spreadsheet to simulate five throws of his biased (red) coin. The probability of head is $0.964$. He also throws a fair (black) coin five times. He collects data for $614$ trials as shown below. The image also shows the outcome of the $614\mathrm{th}$ trial.

Let $R$ and $B$ represent the number of heads in five throws of the red coin and five throws of the black coin respectively.

Find $E\left(R\right)$ and $E\left(B\right)$ and interpret your results.

Calcair buys a new passenger jet with $538$ seats. For the first flight of the new jet all $538$ tickets are sold. Assume that the probability that an individual passenger turns up to the airport in time to take their seat on the jet is $0.91$. Let random variable $T=$the number of passengers that arrive on time to take their seats, stating any assumptions you make. Determine the number of tickets Calcair should sell so that the expected number of passengers turning up on time is as close to $538$ as possible. (Write answer nearest to integer)

In a mathematics competition, students try to find the correct answer from five options in a multiple choice exam of $25$ questions. Alex decides his best strategy is to guess all the answers. Let random variable $A=$the number of questions Alex gets correct. In this test, a correct answer is awarded $4$ points. An incorrect answer incurs a penalty of $1$ point. If Alex guesses all questions, find the expected value of his total points for the examination.

In a mathematics competition, students try to find the correct answer from five options in a multiple choice exam of $25$ questions. Alex decides his best strategy is to guess all the answers. Let random variable $A=$the number of questions Alex gets correct. Write down $E\left(A\right)$ and interpret this value.

A fair octahedral die numbered $1, 2, ....., 8$ is thrown seven times. Let $Q$ denote the number of prime numbers thrown. Find $E\left(Q\right)$.

Given $X~B\left(6, 0.29\right)$ find $E\left(X\right)$.

(Write answer in decimal form, round up to $2$ decimal places)

Given that $\mathrm{X}~\mathrm{B}\left(\mathrm{n}=10,\mathrm{p}\right)$. If $\mathrm{E}\left(\mathrm{X}\right)=8$ find the value of $\mathrm{p}$.

Let $X~B\left(n, p\right), \text{If} n=10, E\left(X\right)=5,$ then find $p$.

If $A$ and $B$ throw a die alternatively till one of them gets $5$ and wins the game. Then the probability of winning by $A$ is _____.

If the mean and variance of a binomial variable $X$ are $2.4$ and $1.44$ respectively, find the parameter $n$ of the distribution $X$. (Binomial).

Given that $\mathrm{X}~\mathrm{B}\left(\mathrm{n}=10,\mathrm{p}\right)$. If $\mathrm{E}\left(\mathrm{X}\right)=8$ find the value of $\mathrm{p}$.

For binomial distribution with mean $6$ and variance $2$, the first two terms of the distribution are

If $x$ is a binomial variate with mean $6$ and variance $2$, then the value of $P\left(5\le x\le 7\right)$ is

If the probability function of a random variable $X$ is defined by $P\left(X=k\right)=a\left(\frac{k+1}{2^k}\right)$ for $k=0, 1, 2, 3, 4, 5$. Then, the probability that $X$ takes a prime value is