Sign of Quadratic Expressions

If $x^2+2ax+10-3a >0$ for all $x \in R$, then

If $b^2-4ac>0$ then the graph of $y=a{x}^2+bx+c$

If the equation $a{x}^2+2bx-3c=0$ has no real roots and $4\left(a+b\right)>3c$, then

The equation $\sin x=x^2+x+1$ has-

Find the real values of $x$ for which $(x^2-4x+1)$ is always negative.

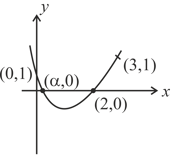
Graph of the function $f\left(x\right)=A{x}^2-Bx+C$, where $A=\left(\sec \theta -\cos \theta \right) \left(\mathrm{cosec}\theta -\sin \theta \right) \left(\tan \theta +\cot \theta \right)$, $B={\left(\sin \theta +\mathrm{cosec}\theta \right)}^2+{\left(\cos \theta +\sec \theta \right)}^2-\left({\tan }^2\theta +{\cot }^2\theta \right)$ and $C=12$, is represented by

The graph of quadratic polynomial $f\left(x\right)=(a-x)(x-b)$ where, $a, b>0$ and $a\ne b$, does not pass through

If $a\in \left(m,n\right)$, then the sign of $x^2-(a+2)x+4$ is always positive. Find the value of $-m+n$?

Find the least integral value of $k$ for which, $\left(k-2\right)x^2+8x+k+4>0$ for all $x\in R.$

If $x^2+2\mathrm{px}-2\mathrm{p}+8>0$ for all real values of $x$ then the set of all possible values of $p$ is

The exhaustive range of $\mathrm{\lambda }$ for which $\mathrm{\lambda }{x}^2>7x-\lambda , \forall x\in R$ , is:

For all $x\in R,$ if  $m{x}^2+\left(5m+1\right)>9mx,$ then $m$ lies in the interval _____

If $\alpha \in R^{-}$ and $\left(\alpha –2\right)x^2+8x+\alpha +4<0,\forall x\in R,$ then $\alpha$ cannot be ____

Consider the quadratic equation: $x^2-2\left(4k-1\right)x+15k^2-2k-7>0 \forall x ϵ R$ .Find the integral value of $k$

Find the number of integral values of $k$ for which ${\mathrm{x}}^2-2(4\mathrm{k}-1)\mathrm{x}+15{\mathrm{k}}^2-2\mathrm{k}-7\ge 0$ hold for all real $x$.

Find least integral value of $k$ such that $(k-2)x^2+8x+k+4$ is positive for all real values of $x$.

Find the largest integral value of $m$ for which the quadratic expression $y=x^2+\left(2m+4\right)x+7m+8$ is positive for all $x\in R$

Statement 1: The probability that $y=16x^2+8(a+5)x-7a-5$ defined in $\left[-26, 0\right]$ is strictly above the $x$-axis is $\frac{1}{2}$.

Statement 2: If the graph of $y=a{x}^2+bx+c$ is strictly above the $x$-axis, then discriminant is negative and $a>0$.

For given figure of $y=f\left(x\right)=a{x}^2+bx+c$,

If graph of $f\left(x\right)=a{x}^2+bx+c$ is given by :