Types of Discontinuity
Types of Discontinuity: Overview
This topic covers concepts, such as, Discontinuity of a Function, Reasons for Discontinuity of a Function at a Point, Jump of Non-removable Discontinuity & Oscillatory Discontinuity etc.
Important Questions on Types of Discontinuity
Function has oscillatory discontinuity at point .
Function has oscillatory discontinuity at point .
Define the oscillatory discontinuity with one example.
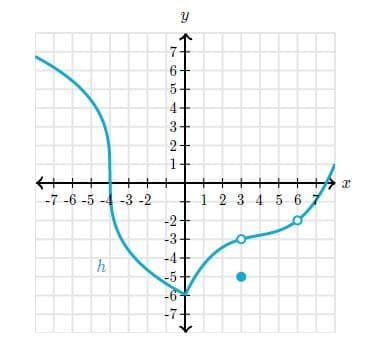
This is the graph of a function .
Find the -value at which has an isolated point discontinuity.
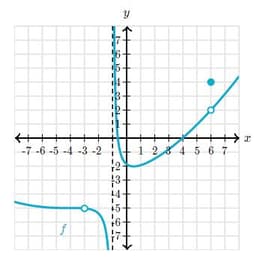
This is the graph of a function .
Find the -value at which has a isolated point discontinuity.
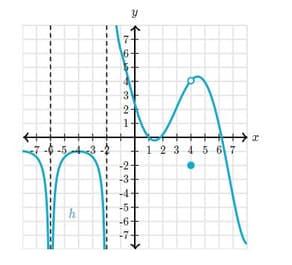
This is the graph of a function . Dashed lines represent asymptotes.
Select the -value at which has an isolated point discontinuity.
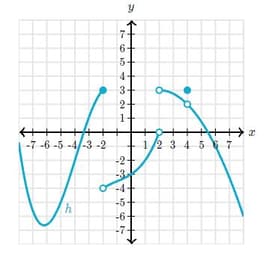
This is the graph of a function .
Find the -value at which has a isolated point discontinuity.
This is the graph of a function .
Find the -value at which has a missing point discontinuity.
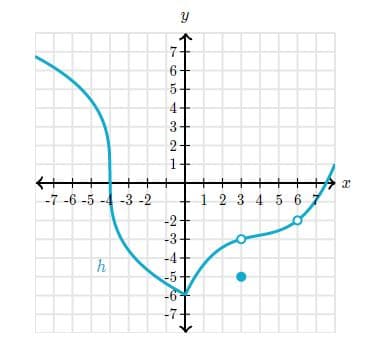
This is the graph of a function . Dashed lines represent asymptotes.
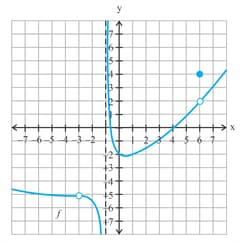
Select the -value at which has a missing point discontinuity.
Let function .
The function has a missing point discontinuity at .
Let function .
The function has a missing point discontinuity at . Find the value of .
Define the missing point discontinuity with one example.
If [.] denotes the Greatest integer function, then is discontinuous at
The function is :
Let , then the numbers of points where is discontinuous is
A point in the domain that cannot be filled in so that the resulting function is continuous is called
If , the number of points of discontinuity of is
Let If and represents number of points, where is discontinuous and non differentiable respectively, then equals
If and , we can uniquely write where and . We define for example . The number of points of discontinuity of the function in the interval is
Consider and If denotes number of points where is discontinuous and non-differentiable respectively in , then value of is